题目内容
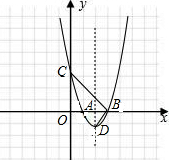 把抛物线y=x2向右、向下平移,使它经过点A(1,0)且与x轴的另一个交点B在A的右侧,与y轴交于点C,如图所示.
把抛物线y=x2向右、向下平移,使它经过点A(1,0)且与x轴的另一个交点B在A的右侧,与y轴交于点C,如图所示.(1)求∠ABC的度数;
(2)设D是平移后抛物线的顶点,若BD⊥BC,试确定平移的方法.
分析:(1)设B(a,0),(a>1),由交点式可知平移后抛物线解析式为y=(x-1)(x-a)=x2-(a+1)x+a,可知抛物线与y轴的交点坐标C(0,a),即OB=OC=a,可求∠ABC的度数;
(2)由|AB|=a-1,可推出∠ABD=45°,故D点坐标为(1+
,-
),再代入抛物线解析式求a,确定顶点坐标和平移方法.
(2)由|AB|=a-1,可推出∠ABD=45°,故D点坐标为(1+
| a-1 |
| 2 |
| a-1 |
| 2 |
解答:解:(1)设B(a,0),(a>1),
则平移后抛物线解析式为y=(x-1)(x-a)=x2-(a+1)x+a,
∴抛物线与y轴的交点坐标C(0,a),
即OB=OC=a,
∠ABC=45°;
(2)根据题意,得|AB|=a-1,
∠ABD=∠CBD-∠ABC=45°,
∴D点坐标为(1+
,-
),即(
,-
),
代入抛物线y=(x-1)(x-a)中,得
(
-1)(
-a)=-
,
解得a=3,
∴D(2,-1),
故抛物线y=x2向右平移2个单位,再向下平移1个单位,得到新抛物线.

则平移后抛物线解析式为y=(x-1)(x-a)=x2-(a+1)x+a,
∴抛物线与y轴的交点坐标C(0,a),
即OB=OC=a,
∠ABC=45°;
(2)根据题意,得|AB|=a-1,
∠ABD=∠CBD-∠ABC=45°,
∴D点坐标为(1+
| a-1 |
| 2 |
| a-1 |
| 2 |
| a+1 |
| 2 |
| a-1 |
| 2 |
代入抛物线y=(x-1)(x-a)中,得
(
| a+1 |
| 2 |
| a+1 |
| 2 |
| a-1 |
| 2 |
解得a=3,
∴D(2,-1),
故抛物线y=x2向右平移2个单位,再向下平移1个单位,得到新抛物线.

点评:本题主要考查了函数图象的平移,抛物线与坐标轴的交点坐标的求法,要求熟练掌握平移的规律:左加右减,上加下减.并用规律求函数解析式.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目