题目内容
【题目】如图,在![]() 的正方形网格中,每个小正方形的边长均为1.
的正方形网格中,每个小正方形的边长均为1.![]() ,
,![]() ,
,![]() ,
,![]() 均在格点上,完成下列问题:
均在格点上,完成下列问题:
(1)四边形![]() 周长是 ;
周长是 ;
(2)四边形![]() 面积是 ;
面积是 ;
(3)求![]() 的度数.
的度数.

【答案】(1)![]() ;(2)
;(2)![]() ;(3)∠DAB=90°.
;(3)∠DAB=90°.
【解析】
(1)借助网格构建直角三角形,利用勾股定理即可分别求出AD、DC、BC、AB,从而求得四边形ABCD的周长;
(2)四边形ABCD的面积等于正方形面积减去四个小三角形面积,据此可得;
(3)求得BD的长度,借助勾股定理逆定理可得△ABD为直角三角形,∠DAB=90°.
解:(1)如下图,由网格可知△AED为直角三角形,
根据勾股定理![]() ,
,
同理可得![]() ,
,![]() ,
,![]()
故四边形![]() 周长=
周长=![]() .
.
故答案为:![]() ;
;
(2)如下图,连接BG
![]()
=![]()
=![]() .
.
故答案为:![]() ;
;
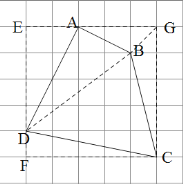
(3)连接BD,根据勾股定理
![]() ,
,![]() ,
,![]() ,
,
∵![]() ,
,
∴△ABD为直角三角形,∠DAB=90°.

练习册系列答案
相关题目