题目内容
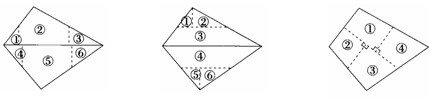
(本小题10分)在平面直角坐标系中.已知O坐标原点.点A(3.0),B(0,4).以点A为旋转中心,把△ABO顺时针旋转,得△ACD.记旋转转角为α.∠ABO为β.
(I) 如图①,当旋转后点D恰好落在AB边上时.求点D的坐标;
(Ⅱ) 如图②,当旋转后满足BC∥x轴时.求α与β之闻的数量关系;
(Ⅲ) 当旋转后满足∠AOD=β时.求直线CD的解析式(直接写出即如果即可),
(I) 如图①,当旋转后点D恰好落在AB边上时.求点D的坐标;
(Ⅱ) 如图②,当旋转后满足BC∥x轴时.求α与β之闻的数量关系;
(Ⅲ) 当旋转后满足∠AOD=β时.求直线CD的解析式(直接写出即如果即可),

解:(I)∵点A(3,0).B(0,4).得0A=3,OB=4.
∴在Rt△ABO中.由勾股定理.得AB=5,
根据题意,有DA=OA=3
如图①.过点D作DM⊥x轴于点M,

则MD∥OB.
∴△ADM∽△ABO。有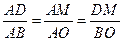 ,
,
得
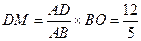
又OM=OA-AM,得OM=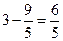 .
.
∴点D的坐标为( )
)
(Ⅱ)如图②.由己知,得∠CAB=α,AC=AB,
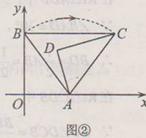
∴∠ABC=∠ACB.
∴在△ABC中,由∠ABC+∠ACB+∠CAB=180°,
得α=180°—2∠ABC,.
又∵BC∥x轴,得∠OBC=90°,
有∠ABC=90°—∠ABO=90°—β
∴α=2β.
(Ⅲ)直线CD的解析式为, 或
或 .
.
∴在Rt△ABO中.由勾股定理.得AB=5,
根据题意,有DA=OA=3
如图①.过点D作DM⊥x轴于点M,

则MD∥OB.
∴△ADM∽△ABO。有
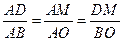 ,
,得

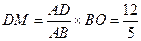
又OM=OA-AM,得OM=
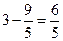 .
.∴点D的坐标为(
 )
)(Ⅱ)如图②.由己知,得∠CAB=α,AC=AB,

∴∠ABC=∠ACB.
∴在△ABC中,由∠ABC+∠ACB+∠CAB=180°,
得α=180°—2∠ABC,.
又∵BC∥x轴,得∠OBC=90°,
有∠ABC=90°—∠ABO=90°—β
∴α=2β.
(Ⅲ)直线CD的解析式为,
 或
或 .
.略

练习册系列答案
相关题目

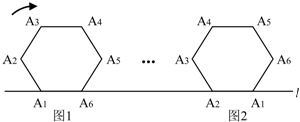






 的正六边形A1 A2 A3 A4 A5 A6在直线
的正六边形A1 A2 A3 A4 A5 A6在直线 上由图1的位置按顺时针
上由图1的位置按顺时针