题目内容
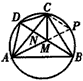
如图,已知圆内接四边形ABCD的对角线AC、BD交于点N,点M在对角线BD上,且满足∠BAM=∠DAN,∠BCM=∠DCN。
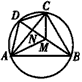
求证:(1)M为BD的中点;
(2)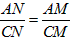 。
。
(2)
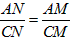 。
。| 解:根据同弧所对的圆周角相等,得∠DAN=∠DBC,∠DCN=∠DBA, 又因为∠DAN=∠BAM,∠BCM=∠DCN, 所以,∠BAM=∠MBC,∠ABM=∠BCM, 有△BAM∽△CBM,则 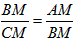 又∠DCM=∠DCN+∠NCM=∠BCM+∠NCM=∠ACB=∠ADB, ∠DAM=∠MAC+∠DAN=∠MAC+∠BAM=∠BAC=∠CDM, 有△DAM∽△CDN,则 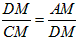 ,即DM2=AM·CM②, ,即DM2=AM·CM②,由式①、②得BM=DM,即M为BD的中点; (2)如图,延长AM交圆于点P,联结CP,则∠BCP=∠PAB=∠DAC=∠DBC, 知PC∥BD,故 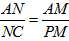 ③, ③,又∠MCB=∠DCA=∠ABD,∠DBC=∠PCB, 所以,∠ABC=∠MCP, 而∠ABC=∠APC,则∠APC=∠MCP,有MP=CM④, 由式③、④得 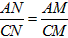 。 。 |
 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
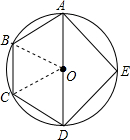 如图,已知圆内接四边形ABCD中,对角线AD是⊙O的直径,AB=BC=CD=2,E是
如图,已知圆内接四边形ABCD中,对角线AD是⊙O的直径,AB=BC=CD=2,E是
 BCM=∠DCN.
BCM=∠DCN. BCM=∠DCN.
BCM=∠DCN.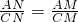 .
.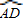 的中点,则△ADE的面积是 .
的中点,则△ADE的面积是 .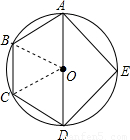
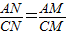 .
.