Question

下列说法：①有两个底角相等的梯形是等腰梯形；②两组对角分别互补的四边形一定是等腰梯形；③一组对角互补的梯形是等腰梯形；④有两个角等于80°的梯形是等腰梯形．其中正确的有

1. A.
   1个
2. B.
   2个
3. C.
   3个
4. D.
   4个

Answer 1

B
分析：根据直角梯形的不等腰即可判断①；根据平行线的性质推出∠A+∠B=180°，推出∠A=∠D即可判断②③；假如∠B=∠D=80°，不符合等腰梯形的判定即可判断④．
解答：①可能是直角梯形，∴①错误；
②两组对角分别互补的四边形可能是矩形，∴②错误
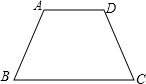③∵AD∥BC，
∴∠A+∠B=180°，
∵∠B+∠D=180°，
∴∠A=∠D，
∵四边形ABCD是梯形，
∴四边形ABCD是等腰梯形，∴③正确；
④若∠B=∠D=80°，由梯形定义，AD∥BC，有∠A=∠C=100°，则ABCD是平行四边形，不是梯形，∴∠B=∠C=80°，∴四边形ABCD是等腰梯形，∴④正确．
故选B．
点评：本题主要考查对等腰梯形的判定，平行线的性质，直角梯形等知识点的理解和掌握，能熟练地根据性质进行推理是解此题的关键．