题目内容
【题目】如图，
,OA=OB=6，点C,D分别为线段OA,OB上的动点（C,D不与A,B重合），则AD+CD+BC的最小值为（ ）
A.4B.6C.
D.
【答案】B
【解析】
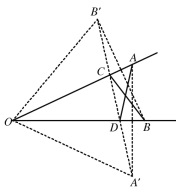
作A关于ON的对称点A'，作B关于OM的对称点B'，连接A'B'交ON、OM于C、D，，此时AD+CD+BC最小，再连接O B'，O A'，可得△O A' B'为等边三角形，则最小值为6.
如图所示，作A关于ON的对称点A'，作B关于OM的对称点B'，连接A'B'交ON、OM于C、D，，此时AD+CD+BC最小值为A' B'，连接O B'，O A'，
由轴对称可知，O B'=OB=6，O A'=OA=6，∠B'OC=∠COD=∠A'OD=20°，
∠B'O A'=60°，而O B'= O A'，∴△O A' B'为等边三角形，∴A' B'=6，即AD+CD+BC的最小值为6，故选B.
练习册系列答案
相关题目
