题目内容
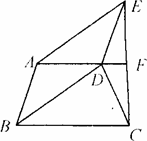
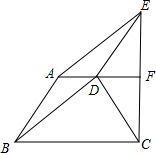如图是某城市部分街道，AF∥BC，EC⊥BC，AB∥DE，BD∥AE，甲、乙两人同时从B站乘车到F站，甲沿B、A、E、F，乙沿B、D、E、F，设两车的速度相同，途中耽误时间相同，那么谁先到达F站，请加以证明？
同时到达F站．
证明：∵AB∥DE，BD∥AE，
∴四边形ABDE是平行四边形，
∴AB=DE，AE=BD，
∴AB+AE+EF=BD+DE+EF，
即：如果两车的速度相同，途中耽误时间相同，那么甲乙两人同时到达F站．
分析：由AB∥DE，BD∥AE，证出?ABDE，得到AB=DE，AE=BD，即可得出答案．
点评：本题考查了平行四边形的性质和判定，解此题的关键是证AB+AE+EF和BD+DE+EF相等．
证明：∵AB∥DE，BD∥AE，
∴四边形ABDE是平行四边形，
∴AB=DE，AE=BD，
∴AB+AE+EF=BD+DE+EF，
即：如果两车的速度相同，途中耽误时间相同，那么甲乙两人同时到达F站．
分析：由AB∥DE，BD∥AE，证出?ABDE，得到AB=DE，AE=BD，即可得出答案．
点评：本题考查了平行四边形的性质和判定，解此题的关键是证AB+AE+EF和BD+DE+EF相等．
练习册系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目
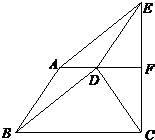23、如图是某城市部分街道，AF∥BC，EC⊥BC，AB∥DE，BD∥AE，甲、乙两人同时从B站乘车到F站，甲沿B、A、E、F，乙沿B、D、E、F，设两车的速度相同，途中耽误时间相同，那么谁先到达F站，请加以证明？
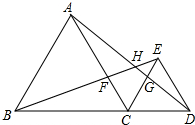如图是某城市的部分街道示意图，AB=BC=AC，CD=CE=DE，A、B、C、D、E、F、G、H为“中巴”停靠点，“中巴”甲从站A出发，按照A→H→G→D→E→C→F的顺序到达F站，“中巴”乙从站B出发，按照B→F→H→E→D→C→G的顺序到达G站，若甲、乙两车同时分别从A、B站出发，在各站停靠的时间、车速均一样，
