题目内容
抛掷红、蓝两枚六面编号分别为0-5(整数)的质地均匀的正方体骰子,将红色和蓝色骰子正面朝上的编号分别作为m和n.
(1)用树状图或列表说明可以得到多少个不同的(m,n)组合;
(2)如果把(m,n)作为点的坐标,求这些点在直线y=x上的概率?
解:列表得:
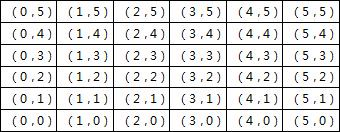
∴(1)可以得到36个不同形式的二次函数(图表略);
(2)点在直线上的有(0,0),(1,1),(2,2),(3,3),(4,4),(5,5)六个,
这样概率为 .
.
分析:此题首先采用列表法求得所有的可能情况共36种,根据一次函数的性质,找出符合点在函数y=x图象上的点有(0,0),(1,1),(2,2),(3,3),(4,4),(5,5)六个,所以这些点在直线y=x上的概率 .
.
点评:列表法可以不重不漏的列举出所有可能发生的情况,用到的知识点为:概率=所求情况数与总情况数之比.

∴(1)可以得到36个不同形式的二次函数(图表略);
(2)点在直线上的有(0,0),(1,1),(2,2),(3,3),(4,4),(5,5)六个,
这样概率为
 .
.分析:此题首先采用列表法求得所有的可能情况共36种,根据一次函数的性质,找出符合点在函数y=x图象上的点有(0,0),(1,1),(2,2),(3,3),(4,4),(5,5)六个,所以这些点在直线y=x上的概率
 .
.点评:列表法可以不重不漏的列举出所有可能发生的情况,用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
 =
= 如图,已知AD∥BC,∠PAB的平分线与∠CBA的平分线相交于E,CE的连线交AP于D.求证:AD+BC=AB.
如图,已知AD∥BC,∠PAB的平分线与∠CBA的平分线相交于E,CE的连线交AP于D.求证:AD+BC=AB. 已知,如图所示,直线AB∥CD,∠AEP=∠CFQ.求证:∠EPM=∠FQM.
已知,如图所示,直线AB∥CD,∠AEP=∠CFQ.求证:∠EPM=∠FQM.
 a2的值是________.
a2的值是________.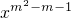 ,当m=________时,它的图象是双曲线.
,当m=________时,它的图象是双曲线.