题目内容
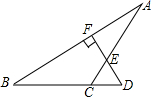如图己知DF⊥AB，∠A=35°，∠D=50°，则∠ACB的度数为
- A.100°
- B.105°
- C.90°
- D.80°
B
分析：由DF与AB垂直，根据垂直定义得到∠BFD=90°，即三角形BFD为直角三角形，根据直角三角形的两个锐角互余，由∠D的度数求出∠B的度数，然后在△ABC中，利用三角形的内角和定理，由∠A和∠B即可求出∠ACB的度数．
解答：∵DF⊥AB，
∴∠BFD=90°，又∠D=50°，
∴∠B=40°，
在△ABC中，根据三角形的内角和定理得：
∠ACB=180°-40°-35°=105°．
故选B
点评：此题考查了三角形的内角和定理，以及垂直的定义．此类题往往需要结合图形，利用三角形的外角性质及三角形的内角和定理找出找出已知角与所求角的关系，进而求出所求角的度数．
分析：由DF与AB垂直，根据垂直定义得到∠BFD=90°，即三角形BFD为直角三角形，根据直角三角形的两个锐角互余，由∠D的度数求出∠B的度数，然后在△ABC中，利用三角形的内角和定理，由∠A和∠B即可求出∠ACB的度数．
解答：∵DF⊥AB，
∴∠BFD=90°，又∠D=50°，
∴∠B=40°，
在△ABC中，根据三角形的内角和定理得：
∠ACB=180°-40°-35°=105°．
故选B
点评：此题考查了三角形的内角和定理，以及垂直的定义．此类题往往需要结合图形，利用三角形的外角性质及三角形的内角和定理找出找出已知角与所求角的关系，进而求出所求角的度数．
练习册系列答案
相关题目
25、在一次数学单元测验中，老师发现小敏同学有一道题只完成了一步，其解答是正确的，遗憾的是她没有做完整．现请你阅读这道题，并完成下列问题：
7、如图己知DF⊥AB，∠A=35°，∠D=50°，则∠ACB的度数为（ ）
