Question

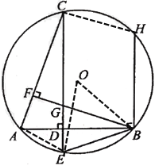
【题目】如图，AB，AC是⊙O的弦，过点C作CE⊥AB于点D，交⊙O于点E，过点B作BF⊥AC于点F，交CE于点G，连接BE。

（1）求证：BE=BG；

（2）过点B作BH⊥AB交⊙O于点H，若BE的长等于半径，BH=4，AC=，求CE的长。

Answer 1

【答案】（1）见解析；（2）6

【解析】

（1）利用圆周角定理、等角的余角相等、等角对等边即可解答；

（2）连接，，，，利用平行线性质、圆内接四边形性质证出四边形是平行四边形，有平行四边形的性质证明是等边三角形，再证明. 设，则AE=2x，因为，，所以，，又因为在中，AD==x.在中，，即，解得，（舍去），所以，即.

（1）证明：∵，

∴.

∵于点，于点，

∴.

∴，

∴，（等角的余角相等）

∴.

（2）解：连接，，，.

∵，

∴，

∴.

∵四边形内接于，

∴，

∴，

∴，

∴四边形是平行四边形，

∴.

∵，

∴是等边三角形，

∴.

∵，

∴.

∵，

∴.

设，则，

∵，，

∴，

∴，

在中，.在中，，

即，解得，（舍去），

∴，

∴.