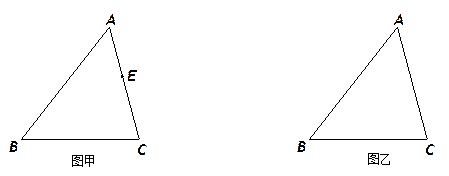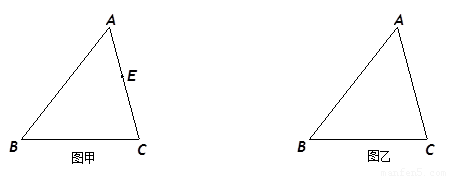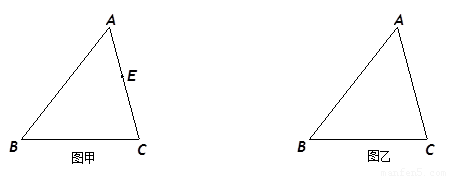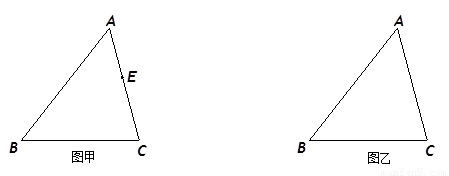题目内容
如图甲,四边形ABCD是等腰梯形,AB∥DC,由4个这样的等腰梯形可以拼出图乙所示的平行四边形.

(1)求梯形ABCD四个内角的度数;
(2)试探究四边形ABCD四条边之间存在的等量关系,并说明理由;
【答案】
(1)∠A=∠B=60°,∠C=∠D=120°;(2)AB=2BC=2CD=2AD.
【解析】
试题分析:(1)根据四边形内角和定理即可求解.
(2)本题要依靠辅助线的帮助,连接MN,求出∠FMN=∠FNM,根据角与边的关系可以求腰长.
(1)如图所示:
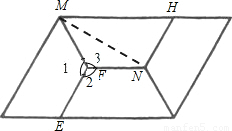
∠1=∠2=∠3,∠1+∠2+∠3=360°,即∠1=120°,
所以∠A=∠B=60°,∠C=∠D=120°;
(2)∵EF既是梯形的腰,又是梯形的上底,
∴梯形的腰等于上底,即MF=FN=EF,
连接MN,
∵∠3=120°,MF=FN,
∴∠FMN=∠FNM==30°,
∴∠HMN=30°,∠HNM=90°,
∴NH= MH,
MH,
∴AB=2BC=2CD=2AD.
考点:等腰梯形的性质,四边形内角和定理
点评:解答本题的关键是认真观察图形,只要善于观察就不难看出底角的三倍等于180°或三个顶角拼成了一个周角.

练习册系列答案
相关题目