题目内容
【题目】从边长为a的大正方形纸板中挖去一个边长为b的小正方形纸板后，将其裁成四个相同的等腰梯形（如图甲），然后拼成一个平行四边形（如图乙）．那么通过计算两个图形阴影部分的面积，可以验证成立的公式为（ ）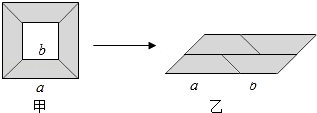 
A.a2﹣b2=（a﹣b）2
B.（a+b）2=a2+2ab+b2
C.（a﹣b）2=a2﹣2ab+b2
D.a2﹣b2=（a+b）（a﹣b）
【答案】D
【解析】解：阴影部分的面积相等，即甲的面积=a2﹣b2 ， 乙的面积=（a+b）（a﹣b）． 即：a2﹣b2=（a+b）（a﹣b）．
所以验证成立的公式为：a2﹣b2=（a+b）（a﹣b）．
故选：D．
【考点精析】通过灵活运用平行四边形的性质和等腰梯形的性质，掌握平行四边形的对边相等且平行；平行四边形的对角相等，邻角互补；平行四边形的对角线互相平分；等腰梯形的两腰相等；同一底上的两个角相等；两条对角线相等即可以解答此题．
练习册系列答案
新思维寒假作业系列答案
相关题目
