题目内容
在一个不透明的布袋中装有四张卡片，四张卡片上分别写有数字：1、2、3、4，若一次性从布袋中抽出其中的两张卡片，试求出两张卡片上的数字之积为偶数的概率（要求用树状图或列表法求解）分析：根据题意可以列出树状图，注意不要漏解，并且是一次抽出两张．
解答：解：方法一：列举所有等可能结果，画出树状图如下：
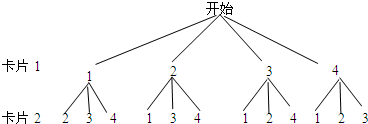
由上图可知，所有等可能结果共有12种，两张卡片上的数字之积为偶数的结果共有10种，
∴P(数字之积为偶数)=
=
（8分）．
解法二：
列表如下
由上表可知，所有等可能结果共有12种，两张卡片上的数字之积为偶数的结果共10种，
∴P(数字之积为偶数)=
=
（8分）．
由上图可知，所有等可能结果共有12种，两张卡片上的数字之积为偶数的结果共有10种，
∴P(数字之积为偶数)=
| 10 |
| 12 |
| 5 |
| 6 |
解法二：
列表如下
| 卡片2 卡片 2 果 结 1 |
1 | 2 | 3 | 4 |
| 1 | （1，2） | （1，3） | （1，4） | |
| 2 | （2，1） | （2，3） | （2，4） | |
| 3 | （3，1） | （3，2） | （3，4） | |
| 4 | （4，1） | （4，2） | （4，3） |
∴P(数字之积为偶数)=
| 10 |
| 12 |
| 5 |
| 6 |
点评：此题主要考查了列表法或树状图求概率，注意列表时它是一次性从布袋中抽出其中的两张卡片这样不可能有重复的卡片．
练习册系列答案
中考解读考点精练系列答案
相关题目