题目内容
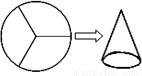
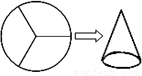
 如图,把一个圆形硬纸片等分成三个扇形,用其中一个扇形制作成一个圆锥形纸筒的侧面(衔接处无缝隙且不重叠),若每一个扇形的面积都是48πcm2,求:
如图,把一个圆形硬纸片等分成三个扇形,用其中一个扇形制作成一个圆锥形纸筒的侧面(衔接处无缝隙且不重叠),若每一个扇形的面积都是48πcm2,求:(1)扇形的弧长;
(2)若另补上圆锥的底部,求圆锥的全面积;
(3)圆锥轴截面底角的正切值.
分析:(1)由每一个扇形的面积都是48πcm2,利用扇形面积公式,即可求得此扇形半径,然后由弧长公式,求得扇形的弧长;
(2)由圆锥的知识,可求得底面圆的半径,继而求得圆锥的全面积;
(3)首先利用勾股定理,求得截面的高,然后由正切函数的定义,即可求得圆锥轴截面底角的正切值.
(2)由圆锥的知识,可求得底面圆的半径,继而求得圆锥的全面积;
(3)首先利用勾股定理,求得截面的高,然后由正切函数的定义,即可求得圆锥轴截面底角的正切值.
解答:解:(1)如图:扇形的圆心角为:
×360°=120°,
根据题意得:S扇形=
=48π(cm2),
∴R=12cm,
∴l扇形=
=
=8π(cm);
∴扇形的弧长为:8πcm;
(2)∵8π=2πr,
∴r=4cm,
∴S全=S侧+S底=48π+π×42=64π(cm2);
∴圆锥的全面积为64πcm2;
(3)∵h=
=
=8
,
∴tanα=
=2
.
∴圆锥轴截面底角的正切值为:2
.
| 1 |
| 3 |
根据题意得:S扇形=
| 120×πR2 |
| 360 |
∴R=12cm,
∴l扇形=
| 120πR |
| 180 |
| 120π×12 |
| 180 |
∴扇形的弧长为:8πcm;
(2)∵8π=2πr,
∴r=4cm,
∴S全=S侧+S底=48π+π×42=64π(cm2);
∴圆锥的全面积为64πcm2;
(3)∵h=
| R2-r2 |
| 122-42 |
| 2 |
∴tanα=
8
| ||
| 4 |
| 2 |
∴圆锥轴截面底角的正切值为:2
| 2 |
点评:此题考查了扇形的面积、弧长公式以及圆锥的有关计算.此题难度适中,注意熟记公式与性质是解此题的关键.

练习册系列答案
相关题目
 (2012•泉港区质检)如图,小刚把一个半径为12cm的圆形硬纸片等分成三个扇形,用其中一个扇形制作成一个圆锥形的纸帽(衔接处无缝隙且不重叠),则圆锥形纸帽的底面圆的半径是
(2012•泉港区质检)如图,小刚把一个半径为12cm的圆形硬纸片等分成三个扇形,用其中一个扇形制作成一个圆锥形的纸帽(衔接处无缝隙且不重叠),则圆锥形纸帽的底面圆的半径是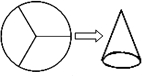 如图,小刚把一个半径为12cm的圆形硬纸片等分成三个扇形,用其中一个扇形制作成一个圆锥形的纸帽(衔接处无缝隙且不重叠),则圆锥形纸帽的底面圆的半径是________cm.
如图,小刚把一个半径为12cm的圆形硬纸片等分成三个扇形,用其中一个扇形制作成一个圆锥形的纸帽(衔接处无缝隙且不重叠),则圆锥形纸帽的底面圆的半径是________cm.