题目内容
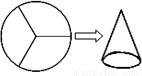
如图,小刚把一个半径为12cm的圆形硬纸片等分成三个扇形,用其中一个扇形制作成一个圆锥形的纸帽(衔接处无缝隙且不重叠),则圆锥形纸帽的底面圆的半径是 cm.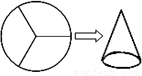
【答案】分析:首先求得圆的周长,利用三等分求得扇形的弧长,利用扇形的弧长等于圆锥底面的周长求得底面的半径即可.
解答:解:∵把一个半径为12cm的圆形硬纸片等分成三个扇形,
∴扇形的弧长为: ×2πr=8π,
×2πr=8π,
∵扇形的弧长等于圆锥的底面周长,
∴2πr=8π,
解得:r=4cm,
故答案为:4
点评:正确理解圆锥的侧面展开图与原来的扇形之间的关系是解决本题的关键,理解圆锥的母线长是扇形的半径,圆锥的底面圆周长是扇形的弧长.
解答:解:∵把一个半径为12cm的圆形硬纸片等分成三个扇形,
∴扇形的弧长为:
 ×2πr=8π,
×2πr=8π,∵扇形的弧长等于圆锥的底面周长,
∴2πr=8π,
解得:r=4cm,
故答案为:4
点评:正确理解圆锥的侧面展开图与原来的扇形之间的关系是解决本题的关键,理解圆锥的母线长是扇形的半径,圆锥的底面圆周长是扇形的弧长.

练习册系列答案
相关题目
 (2012•泉港区质检)如图,小刚把一个半径为12cm的圆形硬纸片等分成三个扇形,用其中一个扇形制作成一个圆锥形的纸帽(衔接处无缝隙且不重叠),则圆锥形纸帽的底面圆的半径是
(2012•泉港区质检)如图,小刚把一个半径为12cm的圆形硬纸片等分成三个扇形,用其中一个扇形制作成一个圆锥形的纸帽(衔接处无缝隙且不重叠),则圆锥形纸帽的底面圆的半径是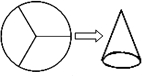 如图,小刚把一个半径为12cm的圆形硬纸片等分成三个扇形,用其中一个扇形制作成一个圆锥形的纸帽(衔接处无缝隙且不重叠),则圆锥形纸帽的底面圆的半径是________cm.
如图,小刚把一个半径为12cm的圆形硬纸片等分成三个扇形,用其中一个扇形制作成一个圆锥形的纸帽(衔接处无缝隙且不重叠),则圆锥形纸帽的底面圆的半径是________cm.