题目内容
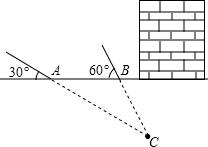
文物探测队探测出某建筑物下面有地下文物,为了准确测出文物所在的深度,他们在文物上方建筑物的一侧地面上相距20米的A、B两处,用仪器测文物C,探测线与地面的夹角分别是30°和60°,求该文物所在位置的深度(精确到0.1米).

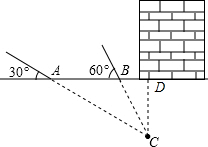
过点C作CD⊥AB于D,设CD=x,
在Rt△ACD中,∠CAD=30°,则AD=
=
x,
在Rt△BCD中,∠CBD=60°,
∵tan∠CBD=
.
∴tan60°=
,
∴BD=
x.
∵AB=AD-BD=20(米),
∴
x-
x=20,
∴x=10
≈17.3(米).
即CD=17.3米.
答:该文物所在的位置在地下约17.3米处.
在Rt△ACD中,∠CAD=30°,则AD=
| CD |
| tan30° |
| 3 |
在Rt△BCD中,∠CBD=60°,
∵tan∠CBD=
| CD |
| BD |
∴tan60°=
| x |
| BD |
∴BD=
| ||
| 3 |
∵AB=AD-BD=20(米),
∴
| 3 |
| ||
| 3 |
∴x=10
| 3 |
即CD=17.3米.
答:该文物所在的位置在地下约17.3米处.


练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
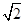 ≈1.414.
≈1.414. ≈1.732)
≈1.732)