题目内容
反比例函数 (
( 为常数)的图象位于
为常数)的图象位于
 (
( 为常数)的图象位于
为常数)的图象位于| A.第一、二象限 | B.第一、三象限 | C.第二、四角限 | D.第三、四象限 |
B
本题考查反比例函数的性质。因为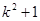 >0,故反比例函数图象经过第一、三象限。故选择B。
>0,故反比例函数图象经过第一、三象限。故选择B。
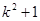 >0,故反比例函数图象经过第一、三象限。故选择B。
>0,故反比例函数图象经过第一、三象限。故选择B。
练习册系列答案
相关题目
题目内容
 (
( 为常数)的图象位于
为常数)的图象位于| A.第一、二象限 | B.第一、三象限 | C.第二、四角限 | D.第三、四象限 |
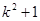 >0,故反比例函数图象经过第一、三象限。故选择B。
>0,故反比例函数图象经过第一、三象限。故选择B。