题目内容
一枚均匀的正方体骰子,六个面分别标有数字:1,2,3,4,5,6.如果用小刚抛掷正方体骰子朝上的数字x,小强抛掷正方体骰子朝上的数字y来确定点P(x,y),那么他们各抛掷一次所确定的点P落在已知直线y=-2x+7图象上的概率是多少?
【答案】分析:根据概率的求法,找准两点:
①符合条件的情况数目;
②全部情况的总数.
二者的比值就是其发生的概率.
解答:解:由题意可得1≤-2x+7≤6,化为不等式组 解得
解得 ≤x≤3.1≤x≤6,且x为正整数,
≤x≤3.1≤x≤6,且x为正整数,
∴x=1,2,3.要使点P落在直线y=-2x+7图象上,则对应的y=5,3,1,
∴满足条件的点P有(1,5),(2,3),(3,1)抛掷骰子所得P点的总个数为36,
∴点P落在直线y=-2x+7图象上的概率P=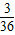 =
=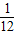 ,
,
答:点P落在直线y=-2x+7图象上的概率是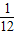 .
.
点评:本题巧妙地把概率、不等式组、一次函数等知识结合在一起,出题思路新颖,别具-格.有利于考查学生灵活应用基础知识解决问题的能力.用到的知识点为:概率=所求情况数与总情况数之比.
①符合条件的情况数目;
②全部情况的总数.
二者的比值就是其发生的概率.
解答:解:由题意可得1≤-2x+7≤6,化为不等式组
 解得
解得 ≤x≤3.1≤x≤6,且x为正整数,
≤x≤3.1≤x≤6,且x为正整数,∴x=1,2,3.要使点P落在直线y=-2x+7图象上,则对应的y=5,3,1,
∴满足条件的点P有(1,5),(2,3),(3,1)抛掷骰子所得P点的总个数为36,
∴点P落在直线y=-2x+7图象上的概率P=
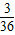 =
=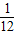 ,
,答:点P落在直线y=-2x+7图象上的概率是
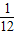 .
.点评:本题巧妙地把概率、不等式组、一次函数等知识结合在一起,出题思路新颖,别具-格.有利于考查学生灵活应用基础知识解决问题的能力.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目
下面有关概率的叙述,正确的是( )
| A、投掷一枚图钉,钉尖朝上的概率和钉尖着地的概率不相同 | ||
B、因为购买彩票时有“中奖”与“不中奖”两种情形,所以购买彩票中奖的概率为
| ||
C、投掷一枚均匀的正方体骰子,每一种点数出现的概率都是
| ||
| D、某种彩票的中奖概率是1%,买100张这样的彩票一定中奖 |
六个人掷一枚均匀的正方体骰子,第( )个人掷出5点的可能性大.
| A、一 | B、三 | C、五 | D、6个人掷出的可能性一样大 |