题目内容
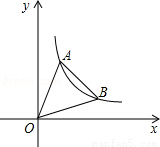
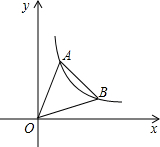
如图,直线y=6x,y= x分别与双曲线y=
x分别与双曲线y=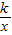 在第一象限内交于点A,B,若S△OAB=8,则k= .
在第一象限内交于点A,B,若S△OAB=8,则k= .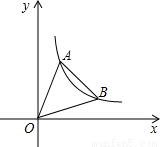
【答案】分析:过点A作AC⊥x轴于点C,过点B作BD⊥x轴于点D,根据双曲线设出点A、B的坐标,并用直线与双曲线解析式联立求出点A、B的横坐标,再根据S△OAB=S△OAC+S梯形ACDB-S△OBD,然后列式整理即可得到关于k的方程,求解即可.
解答: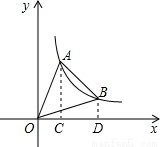 解:如图,过点A作AC⊥x轴于点C,过点B作BD⊥x轴于点D,
解:如图,过点A作AC⊥x轴于点C,过点B作BD⊥x轴于点D,
设点A(x1,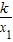 ),B(x2,
),B(x2,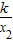 ),
),
联立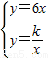 ,解得x1=
,解得x1=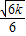 ,
,
联立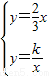 ,解得x2=
,解得x2=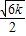 ,
,
S△OAB=S△OAC+S梯形ACDB-S△OBD,
= x1•
x1•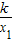 +
+ (
(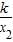 +
+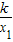 )×(x2-x1)-
)×(x2-x1)- x2•
x2•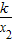 ,
,
= k+
k+ (k-
(k-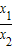 k+
k+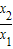 k-k)-
k-k)- k,
k,
= •
• k,
k,
= ×
× k,
k,
= ×
× k,
k,
= k,
k,
∵S△OAB=8,
∴ k=8,
k=8,
解得k=6.
故答案为:6.
点评:本题考查了反比例函数与一次函数的交点问题,反比例函数系数的几何意义,作出辅助线表示出△AOB的面积并整理成只含有k的形式是解题的关键.
解答:
 解:如图,过点A作AC⊥x轴于点C,过点B作BD⊥x轴于点D,
解:如图,过点A作AC⊥x轴于点C,过点B作BD⊥x轴于点D,设点A(x1,
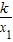 ),B(x2,
),B(x2,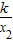 ),
),联立
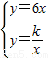 ,解得x1=
,解得x1=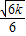 ,
,联立
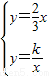 ,解得x2=
,解得x2=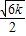 ,
,S△OAB=S△OAC+S梯形ACDB-S△OBD,
=
 x1•
x1•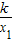 +
+ (
(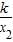 +
+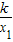 )×(x2-x1)-
)×(x2-x1)- x2•
x2•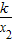 ,
,=
 k+
k+ (k-
(k-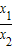 k+
k+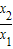 k-k)-
k-k)- k,
k,=
 •
• k,
k,=
 ×
× k,
k,=
 ×
× k,
k,=
 k,
k,∵S△OAB=8,
∴
 k=8,
k=8,解得k=6.
故答案为:6.
点评:本题考查了反比例函数与一次函数的交点问题,反比例函数系数的几何意义,作出辅助线表示出△AOB的面积并整理成只含有k的形式是解题的关键.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
 (2012•十堰)如图,直线y=6x,y=
(2012•十堰)如图,直线y=6x,y= 如图,直线y=6x,y=
如图,直线y=6x,y=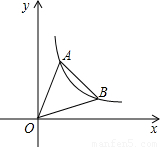
 x分别与双曲线y=
x分别与双曲线y=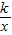 在第一象限内交于点A,B,若S△OAB=8,则k=( )
在第一象限内交于点A,B,若S△OAB=8,则k=( )