题目内容
【题目】如图1,点O在线段AB上,AO=2,OB=1,OC为射线,且∠BOC=60°,动点P以每秒2个单位长度的速度从点O出发,沿射线OC做匀速运动,设运动时间为t秒.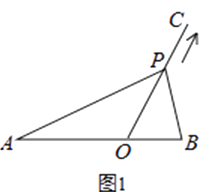
(1)当t= ![]() 秒时,则OP= , S△ABP=;
秒时,则OP= , S△ABP=;
(2)当△ABP是直角三角形时,求t的值;
(3)如图2,当AP=AB时,过点A作AQ∥BP,并使得∠QOP=∠B,求证:AQ·BP=3.为了证明AQ·BP=3,小华同学尝试过O点作OE∥AP交BP于点E.试利用小华同学给我们的启发补全图形并证明AQ·BP=3.
【答案】
(1)1,![]()
(2)解:①∵∠A<∠BOC=60°,
∴∠A不可能是直角.
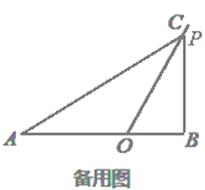
②如备用图,当∠ABP=90°时,
∵∠BOC=60°,
∴∠OPB=30°.
∴OP=2OB,即2t=2.
∴t=1;
③当∠APB=90°,如图1, 
OP=2t,OH=t,PH= ![]() t,AH=2+t,HB=1-t,
t,AH=2+t,HB=1-t,
∵∠APH+∠BPH=90°,∠B+∠BPH=90°,
∴∠APH=∠B.
∴△APH∽△PBH.
∴ ![]() ,即
,即 ![]() ,
,
整理得4t2+t-2=0,
解得t1= ![]() ,t2=
,t2= ![]() (舍去)
(舍去)
(3)解: 补全图形,如图, 
∵AP=AB,
∴∠APB=∠B.
∵OE∥AP,
∴∠OEB=∠APB=∠B.
∵AQ∥BP,
∴∠QAB+∠B=180°.
∵∠OEP+∠OEB=180°,
∴∠OEP=∠QAB.
又∵∠AOC=∠OPB+∠B=∠AOQ+∠QOP,
∵∠B=∠QOP,
∴∠AOQ=∠OPB.
∴△QAO∽△OEP.
∴ ![]() ,即AQEP=EOAO.
,即AQEP=EOAO.
∵OE∥AP,
∴△OBE∽△ABP.
∴ ![]() .
.
∴OE= ![]() AP=1,BP=
AP=1,BP= ![]() EP.
EP.
∴AQBP=AQ ![]() EP=
EP= ![]() AOOE=
AOOE= ![]() ×2×1=3.
×2×1=3.
【解析】解:(1)作PH⊥AB于H, 
∵动点P以每秒2个单位长度的速度从点O出发,
∴当t= ![]() 秒时,则OP=1,
秒时,则OP=1,
∵∠BOC=60°,OP=1,
∴PH=OP×sin60°= ![]() ,
,
∴S△ABP= ![]() ×AB×PH=
×AB×PH= ![]() ,
,
【考点精析】解答此题的关键在于理解相似三角形的判定与性质的相关知识,掌握相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方,以及对解直角三角形的理解,了解解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法).

【题目】某服装店用4400元购进A,B两种新式服装,按标价售出后可获得毛利润2800元(毛利润=售价﹣进价),这两种服装的进价,标价如表所示.
类型价格 | A型 | B型 |
进价(元/件) | 60 | 100 |
标价(元/件) | 100 | 160 |
(1)请利用二元一次方程组求这两种服装各购进的件数;
(2)如果A种服装按标价的9折出售,B种服装按标价的8折出售,那么这批服装全部售完后,服装店比按标价出售少收入多少元?
【题目】为了提高学生书写汉字的能力.增强保护汉字的意识,我区举办了“汉字听写大赛”,经选拔后有50名学生参加决赛,这50名学生同时听写50个汉字,若每正确听写出一个汉字得1分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
组别 | 成绩x分 | 频数(人数) |
第1组 | 25≤x<30 | 4 |
第2组 | 30≤x<35 | 6 |
第3组 | 35≤x<40 | 14 |
第4组 | 40≤x<45 | a |
第5组 | 45≤x<50 | 10 |
请结合图表完成下列各题:
(1)求表中a的值;
(2)请把频数分布直方图补充完整;
(3)若测试成绩不低于40分为优秀,则本次测试的优秀率是多少?



