题目内容
2、如果不等式ax-2a>2-x的解集是x>2,则a的取值范围是
a>-1
.分析:先求解不等式,再根据已知条件即可求出a的取值范围.
解答:解:ax-2a>2-x,
移项得:(a+1)x>2(a+1),
∵解集是x>2,
∴a+1>0,
∴a>-1.
故答案为:a>-1.
移项得:(a+1)x>2(a+1),
∵解集是x>2,
∴a+1>0,
∴a>-1.
故答案为:a>-1.
点评:本题考查了解一元一次不等式,属于基础题,关键是掌握一元一次不等式的性质.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
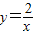 上,那么函数y=(t-1)x+2a的图象不经过第 象限.
上,那么函数y=(t-1)x+2a的图象不经过第 象限.