题目内容
【题目】如果一个三角形的三边a,b,c能满足a2+b2=nc2(n为正整数),那么这个三角形叫做“n阶三角形”.如三边分别为1、2、![]() 的三角形满足12+22=1×(
的三角形满足12+22=1×(![]() )2,所以它是1阶三角形,但同时也满足(
)2,所以它是1阶三角形,但同时也满足(![]() )2+22=9×12,所以它也是9阶三角形.显然,等边三角形是2阶三角形,但2阶三角形不一定是等边三角形.
)2+22=9×12,所以它也是9阶三角形.显然,等边三角形是2阶三角形,但2阶三角形不一定是等边三角形.
(1)在我们熟知的三角形中,何种三角形一定是3阶三角形?
(2)若三边分别是a,b,c(a<b<c)的直角三角形是一个2阶三角形,求a:b:c.
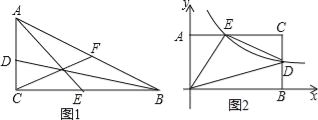
(3)如图1,直角△ABC是2阶三角形,AC<BC<AB,三条中线BD、AE、CF所构成的三角形是何种三角形?四位同学作了猜想:
A同学:是2阶三角形但不是直角三角形;
B同学:是直角三角形但不是2阶三角形;
C同学:既是2阶三角形又是直角三角形;
D同学:既不是2阶三角形也不是直角三角形.
请你判断哪位同学猜想正确,并证明你的判断.
(4)如图2,矩形OACB中,O为坐标原点,A在y轴上,B在x轴上,C点坐标是(2,1),反比例函数y=![]() (k>0)的图象与直线AC、直线BC交于点E、D,若△ODE是5阶三角形,直接写出所有可能的k的值.
(k>0)的图象与直线AC、直线BC交于点E、D,若△ODE是5阶三角形,直接写出所有可能的k的值.
【答案】(1)等腰直角三角形一定是3阶三角形,(2)a:b:c=1:![]() :
:![]() ;(3)C同学猜想正确,(4)满足题意k的值为1,4,7,
;(3)C同学猜想正确,(4)满足题意k的值为1,4,7,![]() .
.
【解析】
试题分析:(1)等腰直角三角形为3阶三角形,根据题中的新定义验证即可;
(2)根据题中的新定义列出关系式,再利用勾股定理列出关系式,即可确定出a,b,c的比值;
(3)C同学猜想正确,由直角△ABC是2阶三角形,根据(2)中的结论得出AC,BC,AB之比,设出三边,表示出AE,BD,CF,利用题中的新定义判断即可;
(4)根据图形设出E与D坐标,利用勾股定理表示出OE2,OD2以及ED2,由△ODE是5阶三角形,分类讨论列出关于k的方程,求出方程的解即可得到k的值
试题解析:(1)等腰直角三角形一定是3阶三角形,
理由为:设等腰直角三角形两直角边为a,a,
根据勾股定理得:斜边为![]() a,
a,
则有a2+(![]() a)2=3a2,即等腰直角三角形一定是3阶三角形;
a)2=3a2,即等腰直角三角形一定是3阶三角形;
(2)∵△ABC为一个2阶直角三角形,
∴c2=a2+b2,且c2+a2=2b2,
两式联立得:2a2+b2=2b2,
整理得:b=![]() a,c=
a,c=![]() a,
a,
则a:b:c=1:![]() :
:![]() ;
;
(3)C同学猜想正确,
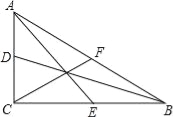
证明如下:如图,∵△ABC为2阶直角三角形,
∴AC:BC:AB=1:![]() :
:![]() ,
,
设BC=2![]() ,AC=2,AB=2
,AC=2,AB=2![]() ,
,
∵AE,BD,CF是Rt△ABC的三条中线,
∴AE2=6,BD2=9,CF2=3,
∴BD2+CF2=2AE2,AE2+CF2=BD2,
∴BD,AE,CF所构成的三角形既是直角三角形,又是2阶三角形;
(4)根据题意设E(k,1),D(2,![]() ),
),
则AE=k,EC=2﹣k,BD=![]() ,CD=1﹣
,CD=1﹣![]() ,OA=1,OB=2,
,OA=1,OB=2,
根据勾股定理得:OE2=1+k2,OD2=4+![]() ,ED2=(2﹣k)2+(1﹣
,ED2=(2﹣k)2+(1﹣![]() )2,
)2,
由△ODE是5阶三角形,分三种情况考虑:
当OE2+OD2=5ED2时,即1+k2+4+![]() =5[(2﹣k)2+(1﹣
=5[(2﹣k)2+(1﹣![]() )2],
)2],
整理得:k2﹣5k+4=0,即(k﹣1)(k﹣4)=0,
解得:k=1或k=4;
当OE2+ED2=5OD2时,(2﹣k)2+(1﹣![]() )2+1+k2=5(4+
)2+1+k2=5(4+![]() ),
),
整理得:k2﹣5k﹣14=0,即(k﹣7)(k+2)=0,
解得:k=7或k=﹣2(舍去);
当OD2+ED2=5OE2时,4+![]() +(2﹣k)2+(1﹣
+(2﹣k)2+(1﹣![]() )2=5(1+k2),
)2=5(1+k2),
整理得:7k2+10k﹣8=0,即(7k﹣4)(k+2)=0,
解得:k=![]() 或k=﹣2(舍去),
或k=﹣2(舍去),
综上,满足题意k的值为1,4,7,![]() .
.

 名校课堂系列答案
名校课堂系列答案