题目内容
某校要从甲、乙两名跳远运动员中挑选一人参加一项校际比赛,在最近的10次选拔赛中,他们的成绩(单位:cm)如下: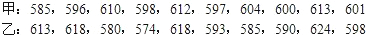
(1)他们的平均成绩分别是多少?
(2)甲、乙这10次比赛成绩的方差分别是多少?
(3)这两名运动员的运动成绩各有什么特点?
(4)历届比赛表明,成绩达到5.96m就很可能夺冠,为夺冠你认为应选谁参加这项比赛?如果历届比赛成绩表明,成绩达6.10m就能打破纪录,那么你认为为了打破纪录选谁参加这项比赛?
分析:根据平均数和方差的概念分别求得甲乙两人的平均数和方差.然后再分析.
解答:解:(1)
甲=
(585+596+610+598+612+597+604+600+613+601)=601.6(cm),
乙=
(613+618+580+574+618+593+585+590+624+598)=599.3(cm);
(2)S甲2=
[(585-601.6)2+(596-601.6)2+(610-601.6)2+(598-601.6)2+(612-601.6)2+(597-601.6)2+(604-601.6)2+(600-601.6)2+(613-601.6)2+(601-601.6)2]=65.84,
S乙2=
[(613-599.3)2+(618-599.3)2+(580-599.3)2+(574-599.3)2+(618-599.3)2+(593-599.3)2+(585-599.3)2+(590-599.3)2+(624-599.3)2+(598-599.3)2]=284.21;
(3)甲的成绩较乙稳定,但乙有几次的成绩特别好,如果发挥的好,乙的成绩比甲好.
(4)为了夺冠应选甲参赛,因为10次比赛中,甲有9次超过5.96米,而乙只有5次;
为了打破记录,应选乙参赛,因为乙超过6.10m有4次,比甲次数多.
. |
| x |
| 1 |
| 10 |
. |
| x |
| 1 |
| 10 |
(2)S甲2=
| 1 |
| 10 |
S乙2=
| 1 |
| 10 |
(3)甲的成绩较乙稳定,但乙有几次的成绩特别好,如果发挥的好,乙的成绩比甲好.
(4)为了夺冠应选甲参赛,因为10次比赛中,甲有9次超过5.96米,而乙只有5次;
为了打破记录,应选乙参赛,因为乙超过6.10m有4次,比甲次数多.
点评:一般地设n个数据,x1,x2,…xn,平均数
=
(x1+x2+x3…+xn),方差S2=
[(x1-
)2+(x2-
)2+…+(xn-
)2]它反映了一组数据的波动大小,方差越大,波动性越大,方差越小,波动性越小.学会分析数据和统计量,从而得出正确的结论.
. |
| x |
| 1 |
| n |
| 1 |
| n |
. |
| x |
. |
| x |
. |
| x |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
某校要从甲、乙两名跳远运动员中挑选一人参加一项校际比赛.在最近的10次选拔赛中,他们的成绩(单位:CM)如下
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 平均分 | 标准差 | |
| 甲 | 585 | 596 | 610 | 598 | 612 | 597 | 604 | 600 | 613 | 601 | 601.6 | |
| 乙 | 613 | 618 | 580 | 574 | 618 | 593 | 585 | 590 | 598 | 624 | 16.86 |
(2)这两名运动员的运动成绩各有什么特点?历届比赛表明,成绩达到5.96m就很可能夺冠,成绩达到6.10m就能打破记录,你认为应该选谁参加这项比赛,请你发表自己的见解.
