Question

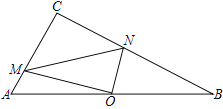
【题目】在Rt△ABC中，∠C＝90°，点O是AB的中点，M、N分别在边AC、BC上，OM⊥ON，连MN，AC＝4，BC＝8．设AM＝a，BN＝b，MN＝c

(1) 求证：a2＋b2＝c2

(2) ① 若a＝1，求b；② 探究a与b之间的函数关系式

(3) △CMN的面积的最大值为__________（不写解答过程）

Answer 1

【答案】(1)见解析；（2）①4.5，②a＋2b＝10；（3）6.

【解析】

（1）过点B作BE∥AC交MO的延长线于E，连接NE，由△AOM≌△BOE，得MO＝OE，AM＝BE＝a，根据垂直平分线的性质得NM＝NE，然后证明△NBE是直角三角形即可；

（2）①根据MN2＝CM2＋CN2，a2＋b2＝c2，列出方程即可解决；

②方法类似①，由c2＝（4a）2＋（8b）2＝a2＋b2可得；

（3）根据S△CMN＝（4a）（8b）＝b2＋11b24，利用二次函数的性质解决问题．

解：（1）证明：如图，过点B作BE∥AC交MO的延长线于E，连接NE．

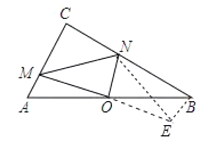
∵AM∥BE，

∴∠A＝∠OBE，

在△AOM和△BOE中，∠A＝∠OBE，AO＝BO，∠AOM＝∠BOE，

∴△AOM≌△BOE，

∴MO＝OE，AM＝BE＝a，

∵OM⊥ON，

∴MN＝NE＝c，

∵∠C＝90°

∴∠A＋∠ABC＝90°，

∴∠OBE＋∠ABC＝90°，

∴∠EBN＝90°，

∴NE2＝BN2＋BE2，

∵NE＝c，BE＝a，BN＝b，

∴a2＋b2＝c2；

（2）①在Rt△MNC中，MN2＝CM2＋CN2，

∴c2＝（4a）2＋（8b）2，∵a＝1，a2＋b2＝c2，

∴1＋b2＝9＋（8b）2，

∴b＝4.5；

②∵c2＝（4a）2＋（8b）2＝a2＋b2，

∴a＋2b＝10．

（3）S△CMN＝（4a）（8b）＝－b2＋11b－24＝，

∵a＋2b＝10，

∵3≤b≤5，

∴当b＝5时，S△CMN最大值＝6．

故答案为6．