题目内容
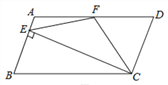
【题目】(满分14分)已知,四边形ABCD是正方形,点F是边AB、BC上一动点,DE⊥DF,且DE=DF,M为EF的中点.
当点F在边AB上时(如图).
求证:点E在BC直线上;
若AD=a,AF=b,并满足![]() .
.
求a,b的值及MC的长;
当点F在BC上时(如图),求![]() 的值.
的值.


(图) (图)
【答案】(1)①见解析,②![]() ;(2)
;(2)![]()
【解析】试题分析:(1)①连接CE,证明△ADF≌△CDE,得到∠DCE=∠DAF=90°即可;②作FK∥MC,证明CM=![]() FK,求出FK=
FK,求出FK=![]() BF即可;(2)过点E作CD的平行线分别交AD、BC的延长线于K、Q,EN∥MC,根据平行线等分线段定理即可解答.
BF即可;(2)过点E作CD的平行线分别交AD、BC的延长线于K、Q,EN∥MC,根据平行线等分线段定理即可解答.
试题解析:
(1)①如图①,连接CE,

∵∠ADC=90°,DE⊥DF,
∴∠ADF=∠CDE,
在△ADF和△CDE中,
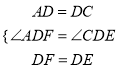 ,
,
∴△ADF≌△CDE,
∴∠DCE=∠DAF=90°,
∴点E在直线BC上;
②如图①,作FK∥MC,∵M为EF的中点,
∴CM=![]() FK,
FK,
∵∠DMB=∠DCB=90°,
∴D、M、C.B四点共圆,
∴∠MCD=∠MBD=45°,
∴∠BKF=45°,
∵BF=2,∴FK=![]() ,
,
∴CM=![]() FK=
FK=![]() ;
;
(2)过点E作CD的平行线分别交AD、BC的延长线于K、G,EN∥MC,
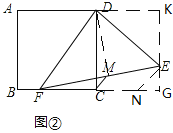
∵M为EF的中点,
∴CM=![]() NE,FC=CN,
NE,FC=CN,
∴NG=EG=BF,
![]() =
=![]() =
=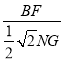 =
=![]() .
.

练习册系列答案
相关题目
【题目】在我县中学生春季田径运动会上,参加男子跳高的16名运动员的成绩如下表所示:
成绩(m) | 1.50 | 1.60 | 1.65 | 1.70 | 1.75 | 1.80 |
人数 | 1 | 3 | 3 | 4 | 3 | 2 |
这些运动员跳高成绩的中位数和众数分别是( )
A.1.70,1.65
B.1.70,1.70
C.1.65,1.70
D.3,3