题目内容
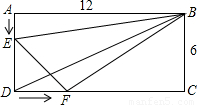
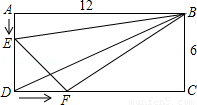
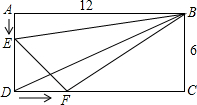
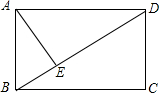 已知如图,在矩形ABCD中,AE⊥BD,垂足为E,∠ADB=30°且BC=4,则△ECD的面积为________.
已知如图,在矩形ABCD中,AE⊥BD,垂足为E,∠ADB=30°且BC=4,则△ECD的面积为________.
2
分析:易证Rt△ABE≌Rt△CDF可得AE=CF,即可得S△ADE=S△CDE,根据勾股定理可以求得BF、FC的值,即可求得△ECD的面积,即可解题.
解答: 解:过C点作CF⊥BD于F,
解:过C点作CF⊥BD于F,
∵∠AEB=∠CFD,∠ABE=∠CDF,AB=CD,
∴Rt△ABE≌Rt△CDF,
得AE=CF,
∴S△ADE=S△ECD,
∵∠ADB=30°,BC=4,
∴AE= BC=2,
BC=2,
∴BF= AE=2
AE=2 ,
,
∴S△ADE= ×BF×FC=2
×BF×FC=2 ,
,
故△ECD的面积为2 ,
,
故答案为 2 .
.
点评:本题考查了勾股定理在直角三角形中的运用,考查了全等三角形的证明和全等三角形对应边相等的性质,本题中计算BF、FC的值是解题的关键.

分析:易证Rt△ABE≌Rt△CDF可得AE=CF,即可得S△ADE=S△CDE,根据勾股定理可以求得BF、FC的值,即可求得△ECD的面积,即可解题.
解答:
 解:过C点作CF⊥BD于F,
解:过C点作CF⊥BD于F,∵∠AEB=∠CFD,∠ABE=∠CDF,AB=CD,
∴Rt△ABE≌Rt△CDF,
得AE=CF,
∴S△ADE=S△ECD,
∵∠ADB=30°,BC=4,
∴AE=
 BC=2,
BC=2,∴BF=
 AE=2
AE=2 ,
,∴S△ADE=
 ×BF×FC=2
×BF×FC=2 ,
,故△ECD的面积为2
 ,
,故答案为 2
 .
.点评:本题考查了勾股定理在直角三角形中的运用,考查了全等三角形的证明和全等三角形对应边相等的性质,本题中计算BF、FC的值是解题的关键.

练习册系列答案
相关题目
 若不能,请说明理由.
若不能,请说明理由.
 若不能,请说明理由.
若不能,请说明理由.