题目内容
甲、乙两人同时从A地沿同一路线走到B地.甲有一半时间以速度a行走,另一半时间以速度b行走;乙有一半路程以速度a行走,另一半路程速度以b行走.设甲、乙两人从A地到B地所走的路程都为S,且a≠b.
(1)试用含a、b、S的式子分别表示甲、乙两人从A地到B地所用的时间t1和t2;
(2)试问甲、乙两人谁先到达B地?并说明理由.
(1)试用含a、b、S的式子分别表示甲、乙两人从A地到B地所用的时间t1和t2;
(2)试问甲、乙两人谁先到达B地?并说明理由.
考点:分式的混合运算
专题:应用题
分析:时间=
,根据甲以一半时间用每小时a千米的速度行走,另一半时间用每小时b千米的速度行走;乙以一半路程用每小时a千米的速度行走,另一半路程用每小时b千米的速度行走,可表示出甲和乙的时间,设路程 是s,甲用的时间是t1,乙用的时间是t2,根据题意可求出解.
| 路程 |
| 速度 |
解答:解:设路程是s,甲用的时间是t1,乙用的时间是t2,
,
解得:
,
当a=b时,
=1,所以同时到达.
当a≠b时,
∵a2-2ab+b2>0,
∴a2+b2>2ab,
∴a2+2ab+b2>4ab,
∴
<1,甲先到达.
|
解得:
|
当a=b时,
| t1 |
| t2 |
当a≠b时,
∵a2-2ab+b2>0,
∴a2+b2>2ab,
∴a2+2ab+b2>4ab,
∴
| t1 |
| t2 |
点评:本题考查理解题意的能力,关键是用速度表示出时间,然后根据a,b速度的相同和不同得出结论.

练习册系列答案
相关题目
若
≈2.872,
≈1.333,则
≈( )
| 3 | 23.7 |
| 3 | 2.37 |
| 3 | 0.0237 |
| A、0.2872 |
| B、0.1333 |
| C、0.01333 |
| D、0.002872 |
分别写有数字-l,-2,0,1,2的五张卡片,除数字不同外其他均相同,从中任抽一张,那么抽到负数的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
 如图中的四边形都是正方形,字母B所代表的正方形的面积是
如图中的四边形都是正方形,字母B所代表的正方形的面积是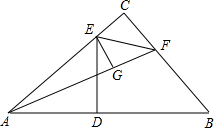 如图,在△ABC中,∠C=90°,AB的垂直平分线DE交AC于点E,垂足是D,F是BC上一点,EF平分∠AFC,EG⊥AF于点G.
如图,在△ABC中,∠C=90°,AB的垂直平分线DE交AC于点E,垂足是D,F是BC上一点,EF平分∠AFC,EG⊥AF于点G.