题目内容
 (2012•湖州)已知:如图,在?ABCD中,点F在AB的延长线上,且BF=AB,连接FD,交BC于点E.
(2012•湖州)已知:如图,在?ABCD中,点F在AB的延长线上,且BF=AB,连接FD,交BC于点E.(1)说明△DCE≌△FBE的理由;
(2)若EC=3,求AD的长.
分析:(1)由四边形ABCD是平行四边形,根据平行四边形的对边平行且相等,即可得AB=DC,AB∥DC,继而可求得∠CDE=∠F,又由BF=AB,即可利用AAS,判定△DCE≌△FBE;
(2)由(1),可得BE=EC,即可求得BC的长,又由平行四边形的对边相等,即可求得AD的长.
(2)由(1),可得BE=EC,即可求得BC的长,又由平行四边形的对边相等,即可求得AD的长.
解答:(1)证明:∵四边形ABCD是平行四边形,
∴AB=DC,AB∥DC,1分
∴∠CDE=∠F,1分
又∵BF=AB,1分
∴DC=FB,
在△DCE和△FBE中,
∵
∴△DCE≌△FBE(AAS)
(2)解:∵△DCE≌△FBE,
∴EB=EC,
∵EC=3,
∴BC=2EB=6,1分
∵四边形ABCD是平行四边形,
∴AD=BC,
∴AD=6.
∴AB=DC,AB∥DC,1分
∴∠CDE=∠F,1分
又∵BF=AB,1分
∴DC=FB,
在△DCE和△FBE中,
∵
|
∴△DCE≌△FBE(AAS)
(2)解:∵△DCE≌△FBE,
∴EB=EC,
∵EC=3,
∴BC=2EB=6,1分
∵四边形ABCD是平行四边形,
∴AD=BC,
∴AD=6.
点评:此题考查了平行四边形的性质与全等三角形的判定与性质.此题难度适中,注意数形结合思想的应用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
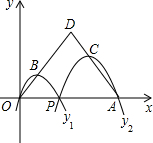 (2012•湖州)如图,已知点A(4,0),O为坐标原点,P是线段OA上任意一点(不含端点O,A),过P、O两点的二次函数y1和过P、A两点的二次函数y2的图象开口均向下,它们的顶点分别为B、C,射线OB与AC相交于点D.当OD=AD=3时,这两个二次函数的最大值之和等于( )
(2012•湖州)如图,已知点A(4,0),O为坐标原点,P是线段OA上任意一点(不含端点O,A),过P、O两点的二次函数y1和过P、A两点的二次函数y2的图象开口均向下,它们的顶点分别为B、C,射线OB与AC相交于点D.当OD=AD=3时,这两个二次函数的最大值之和等于( )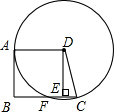 (2012•湖州)已知,如图,在梯形ABCD中,AD∥BC,DA=DC,以点D为圆心,DA长为半径的⊙D与AB相切于A,与BC交于点F,过点D作DE⊥BC,垂足为E.
(2012•湖州)已知,如图,在梯形ABCD中,AD∥BC,DA=DC,以点D为圆心,DA长为半径的⊙D与AB相切于A,与BC交于点F,过点D作DE⊥BC,垂足为E.