题目内容
(2012•资中县模拟)已知一次函数y=
+5的图象与x轴交于A点,y=-
-
的图象与y轴交于B点,这两个一次函数的图象相交于P点,则△ABP的面积是
.
| 4x |
| 3 |
| 3x |
| 2 |
| 7 |
| 2 |
| 51 |
| 16 |
| 51 |
| 16 |
分析:先根据直线解析式求出点A、B的坐标,联立两函数解析式求解得到点P的坐标,设直线y=-
x-
与x轴的交点为C,求出点C的坐标,然后求粗AC的长度,再根据S△ABP=S△APC+S△ABC,列式计算即可得解.
| 3 |
| 2 |
| 7 |
| 2 |
解答: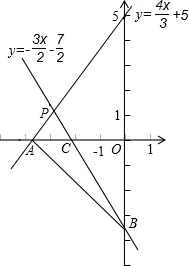 解:令y=0,则
解:令y=0,则
+5=0,
解得x=-
,
令x=0,则y=-
,
所以,点A(-
,0),B(0,-
),
联立
,
解得
,
所以,点P(-3,1),
设直线y=-
x-
与x轴的交点为C,
令y=0,则-
x-
=0,
解得x=-
,
所以,点C(-
,0),
AC=-
-(-
)=-
+
=
,
S△ABP=S△APC+S△ABC,
=
×
×1+
×
×
,
=
+
,
=
.
故答案为:
.
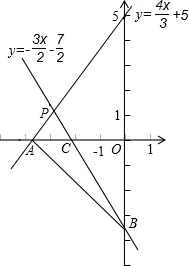 解:令y=0,则
解:令y=0,则| 4x |
| 3 |
解得x=-
| 15 |
| 4 |
令x=0,则y=-
| 7 |
| 2 |
所以,点A(-
| 15 |
| 4 |
| 7 |
| 2 |
联立
|
解得
|
所以,点P(-3,1),
设直线y=-
| 3 |
| 2 |
| 7 |
| 2 |
令y=0,则-
| 3 |
| 2 |
| 7 |
| 2 |
解得x=-
| 7 |
| 3 |
所以,点C(-
| 7 |
| 3 |
AC=-
| 7 |
| 3 |
| 15 |
| 4 |
| 7 |
| 3 |
| 15 |
| 4 |
| 17 |
| 12 |
S△ABP=S△APC+S△ABC,
=
| 1 |
| 2 |
| 17 |
| 12 |
| 1 |
| 2 |
| 17 |
| 12 |
| 7 |
| 2 |
=
| 17 |
| 24 |
| 119 |
| 48 |
=
| 51 |
| 16 |
故答案为:
| 51 |
| 16 |
点评:本题考查了两直线相交的问题,主要涉及直线与坐标轴的交点的求解,联立两直线解析式求交点坐标以及求三角形的面积的方法,难点较大,把△ABP的面积分成两个三角形的面积求解比较关键.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目