题目内容
已知抛物线y＝x2＋bx＋c与直线y＝x＋1有两个交点A、B．
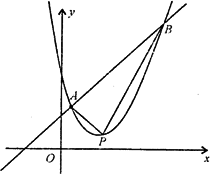
(1)当AB的中点落在y轴时，求c的取值范围；
(2)当AB＝2
，求c的最小值，并写出c取最小值时抛物线的解析式；
(3)设点P(t，T)在AB之间的一段抛物线上运动，S(t)表示△PAB的面积．
①当AB＝2，且抛物线与直线的一个交点在y轴时，求S(t)的最大值，以及此时点P的坐标；
②当AB＝m(正常数)时，S(t)是否仍有最大值，若存在，
求出S(t)的最大值以及此时点P的坐标(t，T)满足的关系，若不存在说明理由．
答案：
练习册系列答案
相关题目
x2＋bx＋c与坐标轴交于A、B、C三点， A点的坐标为（－1，0），过点C的直线y＝
x－3与x轴交于点Q，点P是线段BC上的一个动点，过P作PH⊥OB于点H．若PB＝5t，且0＜t＜1．
x2＋bx＋c与坐标轴交于A、B、C三点， A点的坐标为（－1，0），过点C的直线y＝
x－3与x轴交于点Q，点P是线段BC上的一个动点，过P作PH⊥OB于点H．若PB＝5t，且0＜t＜1．