题目内容
(2009•盐城模拟)如图,四边形ABCD、EFGH、NHMC都是正方形,A、B、N、E、F五点在同一直线上,且正方形ABCD、EFGH面积分别是4和9,则正方形NHMC的面积是 .
【答案】分析:先利用AAS判定△CBN≌△NEH得出BC=NE,BN=EH,再根据两个正方形的面积分别求得其边长,根据勾股定理得到所求的正方形的边长,从而得出所求的面积为13.
解答:解:∵四边形ABCD、EFGH、NHMC都是正方形
∴CN=NH,∠CNH=90°,∠CBN=∠NEH=90°,
∵∠BCN+∠BNC=90°,∠BNC+∠ENH=90°,
∴∠BCN=∠ENH,
∴△CBN≌△NEH(AAS)
∴BC=NE,BN=EH
∵正方形ABCD、EFGH面积分别是4和9,
∴BC=2,BN=3
∴CN=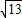
∴正方形NHMC的面积是13.
故填:13.
点评:此题考查了全等三角形的判定,正方形的性质,勾股定理等知识点,有一定的综合性.
解答:解:∵四边形ABCD、EFGH、NHMC都是正方形
∴CN=NH,∠CNH=90°,∠CBN=∠NEH=90°,
∵∠BCN+∠BNC=90°,∠BNC+∠ENH=90°,
∴∠BCN=∠ENH,
∴△CBN≌△NEH(AAS)
∴BC=NE,BN=EH
∵正方形ABCD、EFGH面积分别是4和9,
∴BC=2,BN=3
∴CN=
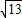
∴正方形NHMC的面积是13.
故填:13.
点评:此题考查了全等三角形的判定,正方形的性质,勾股定理等知识点,有一定的综合性.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
 ,求b的值;
,求b的值;

 .
.