Question

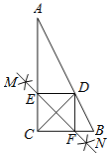
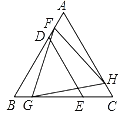
【题目】△BDE和△FGH是两个全等的等边三角形，将它们按如图的方式放置在等边三角形ABC内．若求五边形DECHF的周长，则只需知道（　　）

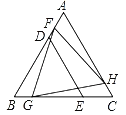
A.△ABC的周长B.△AFH的周长

C.四边形FBGH的周长D.四边形ADEC的周长

Answer 1

【答案】A

【解析】

由等边三角形的性质和三角形的内角和定理可得：FH＝GH，∠ACB＝∠A＝60°，∠AHF＝∠HGC，进而可根据AAS证明△AFH≌△CHG，可得AF＝CH，然后根据等量代换和线段间的和差关系即可推出五边形DECHF的周长＝AB+BC，从而可得结论．

解：∵△GFH为等边三角形，

∴FH＝GH，∠FHG＝60°，

∴∠AHF+∠GHC＝120°，

∵△ABC为等边三角形，

∴AB＝BC＝AC，∠ACB＝∠A＝60°，

∴∠GHC+∠HGC＝120°，

∴∠AHF＝∠HGC，

∴△AFH≌△CHG（AAS），

∴AF＝CH．

∵△BDE和△FGH是两个全等的等边三角形，

∴BE＝FH，

∴五边形DECHF的周长＝DE+CE+CH+FH+DF

＝BD+CE+AF+BE+DF

＝（BD+DF+AF）+（CE+BE），

＝AB+BC．

∴只需知道△ABC的周长即可．

故选：A．