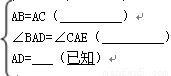题目内容
如图，在AB=AC的△ABC中，D点在AC边上，使BD=BC，E点在AB边上，使AD=DE=EB，求∠EDB.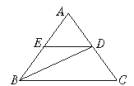
答案：
解析：
解析：
| 设∠BDE=x ∵BE=DE∴∠EBD=∠EDB=x
则∠AED=∠EDB+∠EBD=2x 又∵AD=DE ∴∠A=∠AED=2x 又∠BDC=∠A+∠ABD=3x 又∵BD=BC，∴∠C=∠BDC=3x 又∵AB=AC，∴∠ABC=∠C=3x 根据三角形内角和定理3x+3x+2x=180° ∴x=22.5°
|
练习册系列答案
星级口算天天练系列答案
相关题目
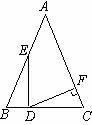
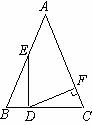
16、如图，在①AB=AC ②AD=AE ③∠B=∠C ④BD=CE四个条件中，能证明△ABD与△ACE全等的条件顺序是（ ）
