题目内容
方程x2－4x＝0的解是
| A．x＝4 | B．x1＝1，x2＝4 | C．x1＝0，x2＝4 | D．x1＝1，x2＝－4 |
C
析：由题已知的方程进行因式分解，将原式化为两式相乘的形式，再根据两式相乘值为0，这两式中至少有一式值为0，求出方程的解．
解答：解：∵x2-4x=0，
∴x（x-4）=0，
∴方程的解：x1=0，x2=4．
故选C．
解答：解：∵x2-4x=0，
∴x（x-4）=0，
∴方程的解：x1=0，x2=4．
故选C．
练习册系列答案
全能测控一本好卷系列答案
相关题目
的一元二次方程中，有两个不相等的实数根的方程是（ ）
，则
= ．
是方程
的一个根，则
，方程的另一个根是 ．
有两个整数根，则整数m = .
的根是
，
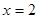
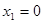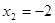
＋2x－2=0
．