题目内容
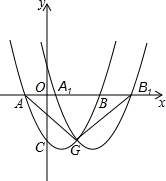 已知抛物线y=x2-2x-3与x轴交于A、B两点,与y轴交于C点,将此抛物线向右平移得y=x2+mx+n,平移后的抛物线与原抛物线的交点为G,与x轴的交点为A1,B1,若△AGB1为等腰直角三角形,求m,n的值.
已知抛物线y=x2-2x-3与x轴交于A、B两点,与y轴交于C点,将此抛物线向右平移得y=x2+mx+n,平移后的抛物线与原抛物线的交点为G,与x轴的交点为A1,B1,若△AGB1为等腰直角三角形,求m,n的值.分析:令y=0,求出点A、B的坐标,从而得到AB的长,设向右平移a个单位,然后根据等腰直角三角形的性质表示出点G的横坐标和纵坐标,再根据点G是两个抛物线的交点,把点G的坐标代入抛物线解析式求出a的值,再求出原抛物线的顶点坐标并根据向右平移横坐标加求出平移后的抛物线的顶点坐标,利用顶点式解析式写出并整理成一般形式,最后根据对应项系数相等求出m、n的值.
解答:解:令y=0,则x2-2x-3=0,
解得x1=-1,x2=3,
∴A(-1,0),B(3,0),
∴AB=3-(-1)=3+1=4,
设向右平移a个单位(a>0),则AB1=4+a,
∵△AGB1为等腰直角三角形,
∴点G的横坐标为
-1=
,
纵坐标为-
,
∵点G是两个抛物线的交点,
∴(
)2-2×
-3=-
,
整理得,a2+2a-8=0,
解得a1=2,a2=-4(舍去),
∵y=x2-2x-3=(x-1)2-4,
∴原抛物线的顶点坐标为(1,-4),
∴平移后抛物线的顶点坐标为(3,-4),
∴平移后的抛物线解析式为y=(x-3)2-4=x2-6x+5,
又∵平移后的抛物线解析式为y=x2+mx+n,
∴m=-6,n=5.
解得x1=-1,x2=3,
∴A(-1,0),B(3,0),
∴AB=3-(-1)=3+1=4,
设向右平移a个单位(a>0),则AB1=4+a,
∵△AGB1为等腰直角三角形,
∴点G的横坐标为
| 4+a |
| 2 |
| 2+a |
| 2 |
纵坐标为-
| 4+a |
| 2 |
∵点G是两个抛物线的交点,
∴(
| 2+a |
| 2 |
| 2+a |
| 2 |
| 4+a |
| 2 |
整理得,a2+2a-8=0,
解得a1=2,a2=-4(舍去),
∵y=x2-2x-3=(x-1)2-4,
∴原抛物线的顶点坐标为(1,-4),
∴平移后抛物线的顶点坐标为(3,-4),
∴平移后的抛物线解析式为y=(x-3)2-4=x2-6x+5,
又∵平移后的抛物线解析式为y=x2+mx+n,
∴m=-6,n=5.
点评:本题是二次函数综合题型,主要利用了等腰直角三角形的性质,二次函数图象与几何变换,利用平移距离表示出点G的横坐标与纵坐标是解题的关键,也是本题的难点.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
已知抛物线y=x2-8x+c的顶点在x轴上,则c等于( )
| A、4 | B、8 | C、-4 | D、16 |
 (1)求b+c的值;
(1)求b+c的值;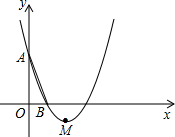 (2012•虹口区一模)如图,在平面直角坐标系xOy中,已知抛物线y=x2+bx+c经过A(0,3),B(1,0)两点,顶点为M.
(2012•虹口区一模)如图,在平面直角坐标系xOy中,已知抛物线y=x2+bx+c经过A(0,3),B(1,0)两点,顶点为M.