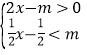题目内容
【题目】写出命题:“等腰三角形两腰上的高相等”的逆命题,并证明其逆命题是真命题.(要求写出已知、求证和证明过程)
 .
.
【答案】一个三角形两边上的高相等,则这个三角形是等腰三角形,证明见解析.
【解析】
(1)交换命题的题设和结论即可写出其逆命题;
(2)通过HL证得Rt△BCD≌Rt△CBE得到∠ABC=∠ACB,则等角对等边:AB=AC,即△ABC是等腰三角形.
逆命题是:一个三角形两边上的高相等,则这个三角形是等腰三角形.
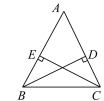
已知:如图,△ABC中,BD⊥AC于点D,CE⊥AB于点E,且BD=CE,
求证:△ABC是等腰三角形.
证明:∵BD⊥AC,CE⊥AB.
∴∠BDC=∠CEB=90°,
又∵BD=CE,BC=CB,
∴Rt△BCD≌Rt△CBE(H.L.),
∴∠BCD=∠CBE,
∴AB=AC,
∴△ABC是等腰三角形

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目