题目内容
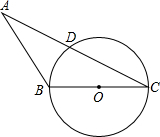（2012•大庆）如图△ABC中，BC=3，以BC为直径的⊙O交AC于点D，若D是AC中点，∠ABC=120°．（1）求∠ACB的大小；
（2）求点A到直线BC的距离．
分析：（1）根据垂直平分线的性质得出AB=BC，进而得出∠A=∠C=30°即可；
（2）根据BC=3，∠ACB=30°，∠BDC=90°，得出CD的长，进而求出AE的长度即可．
（2）根据BC=3，∠ACB=30°，∠BDC=90°，得出CD的长，进而求出AE的长度即可．
解答：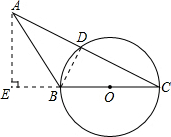
解：（1）连接BD，
∵以BC为直径的⊙O交AC于点D，
∴∠BDC=90°，
∵D是AC中点，
∴BD是AC的垂直平分线，
∴AB=BC，
∴∠A=∠C，
∵∠ABC=120°，
∴∠A=∠C=30°，
即∠ACB=30°；
（2）过点A作AE⊥BC于点E，
∵BC=3，∠ACB=30°，∠BDC=90°，
∴cos30°=
=
，
∴CD=
，
∵AD=CD，
∴AC=3
，
∵在Rt△AEC中，∠ACE=30°，
∴AE=
×3
=
．
解：（1）连接BD，∵以BC为直径的⊙O交AC于点D，
∴∠BDC=90°，
∵D是AC中点，
∴BD是AC的垂直平分线，
∴AB=BC，
∴∠A=∠C，
∵∠ABC=120°，
∴∠A=∠C=30°，
即∠ACB=30°；
（2）过点A作AE⊥BC于点E，
∵BC=3，∠ACB=30°，∠BDC=90°，
∴cos30°=
| CD |
| BC |
| CD |
| 3 |
∴CD=
3
| ||
| 2 |
∵AD=CD，
∴AC=3
| 3 |
∵在Rt△AEC中，∠ACE=30°，
∴AE=
| 1 |
| 2 |
| 3 |
3
| ||
| 2 |
点评：此题主要考查了圆周角定理、等腰三角形的判定与性质、含30度角的直角三角形的性质，根据已知得出CD的长度是解题关键．
练习册系列答案
相关题目
（2012•大庆）如图所示，将一个圆盘四等分，并把四个区域分别标上I、Ⅱ、Ⅲ、Ⅳ，只有区域I为感应区域，中心角为60°的扇形AOB绕点0转动，在其半径OA上装有带指示灯的感应装置，当扇形AOB与区域I有重叠（原点除外）的部分时，指示灯会发光，否则不发光，当扇形AOB任意转动时，指示灯发光的概率为（ ）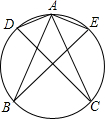
（2012•大庆）如图所示，已知△ACD和△ABE都内接于同一个圆，则∠ADC+∠AEB+∠BAC=（ ）
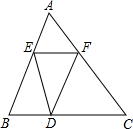（2012•大庆）如图所示，△ABC中，E、F、D分别是边AB、AC、BC上的点，且满足