题目内容
【题目】对于一次函数y=kx+b(k≠0),我们称函数y[m]=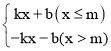 为它的m分函数(其中m为常数).例如,y=3x+2的4分函数为:当x≤4时,y[4]=3x+2;当x>4时,y[4]=-3x-2.
为它的m分函数(其中m为常数).例如,y=3x+2的4分函数为:当x≤4时,y[4]=3x+2;当x>4时,y[4]=-3x-2.
(1)如果y=x+1的-1分函数为y[-1],
①当x=4时,y[-1]______;当y[-1]=-3时,x=______.
②求双曲线y=![]() 与y[-1]的图象的交点坐标;
与y[-1]的图象的交点坐标;
(2)如果y=-x+2的0分函数为y[0],正比例函数y=kx(k≠0)与y=-x+2的0分函数y[0]的图象无交点时,直接写出k的取值范围.
【答案】(1)①5,-4或2;②(-2,-1);(2)k≥1
【解析】
(1)①先写出函数的-1分函数,代入即可,注意,函数值时-3时分两种情况代入;
②先写出函数的-1分函数,分两种情况和双曲线解析式联立求解即可;
(2)先写出函数的0分函数,画出图象,根据图象即可求得.
解:(1)①y=x+1的-1分函数为:当x≤-1时,y[-1]=x+1;当x>-1时,y[-1]=-x-1.
当x=4时,y[-1]=-4-1=-5,
当y[-1]=-3时,
如果x≤-1,则有,x+1=-3,
∴x=-4,
如果x>-1,则有,-x-1=-3,
∴x=2,
故答案为-5,-4或2;
②当y=x+1的-1分函数为y[-1],
∴当x≤-1时,y[-1]=x+1①,
当x>-1时,y[-1]=-x-1②,
∵双曲线y=![]() ③,
③,
联立①③解得,![]() (舍)
(舍)![]() ,
,
∴它们的交点坐标为(-2,-1),
联立②③时,方程无解,
∴双曲线y=![]() 与y[-1]的图象的交点坐标(-2,-1);
与y[-1]的图象的交点坐标(-2,-1);
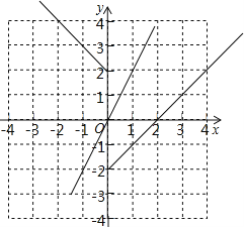
(2)当y=-x+2的0分函数为y[0],
∴当x≤0时,y[0]=-x+2,
当x>0时,y[0]=x-2,如图,
∵正比例函数y=kx(k≠0)与y=-x+2的0分函数y[0]的图象无交点,
∴k≥1.

 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案【题目】小军和小刚两位同学在学习”概率“时,做投掷骰子(质地均匀的正方体)实验,他们共做了60次试验,实验的结果如下:
向上点数 | 1 | 2 | 3 | 4 | 5 | 6 |
出现次数 | 7 | 9 | 6 | 8 | 20 | 10 |
(1)计算“2点朝上”的频率和“5点朝上”的频率.
(2)小军说:“根据实验,一次实验中出现3点朝上的概率是![]() ”;小军的这一说法正确吗?为什么?
”;小军的这一说法正确吗?为什么?
(3)小刚说:“如果掷600次,那么出现6点朝上的次数正好是100次.”小刚的这一说法正确吗?为什么?