题目内容
如图1,D为线段BC的中点,AD为△ABC中BC边上的中线.
(1)求证:S△ADB=S△ADC
探究论证:
(2)如图2,点D、O分别为线段BC、AD的中点,连结BO和CO,设△ABC的面积为S,△ABD的面积为S1,用含S的代数式表示S1,并说明理由;
实际应用:
如图3,学校有一块面积为40m2的△ABC空地,按图3所示分割,其中点D、E、F分别是线段BC、AD、EC的中点,拟计划在△BEF内在中花卉,其余地方铺草坪,则栽种花卉(阴影部分)的面积是
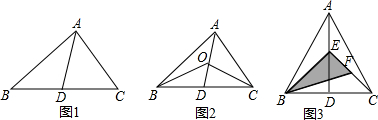
(1)求证:S△ADB=S△ADC
探究论证:
(2)如图2,点D、O分别为线段BC、AD的中点,连结BO和CO,设△ABC的面积为S,△ABD的面积为S1,用含S的代数式表示S1,并说明理由;
实际应用:
如图3,学校有一块面积为40m2的△ABC空地,按图3所示分割,其中点D、E、F分别是线段BC、AD、EC的中点,拟计划在△BEF内在中花卉,其余地方铺草坪,则栽种花卉(阴影部分)的面积是
10
10
m2.
分析:(1)根据三角形中线的性质即可证明S△ADB=S△ADC;
(2)根据三角形中线的性质可得含S的代数式表示S1,根据三角形中线的性质可得栽种花卉(阴影部分)的面积是△ABC面积的
.
(2)根据三角形中线的性质可得含S的代数式表示S1,根据三角形中线的性质可得栽种花卉(阴影部分)的面积是△ABC面积的
| 1 |
| 4 |
解答: 解:(1)作AE⊥BC.
解:(1)作AE⊥BC.
∵S△ADB=BD×AE×
,
S△ADC=CD×AE×
,
又∵AD为△ABC中BC边上的中线,
∴BD=CD,
∴S△ADB=S△ADC;
(2)由(1)可知S△ADB=S△ADC,
同理S△ABO=S△DBO=
S△ADB,
∴S△ABO=
S△ABC,
即S1=
S,
栽种花卉(阴影部分)的面积是
×40=10m2.
故答案为:10.
 解:(1)作AE⊥BC.
解:(1)作AE⊥BC.∵S△ADB=BD×AE×
| 1 |
| 2 |
S△ADC=CD×AE×
| 1 |
| 2 |
又∵AD为△ABC中BC边上的中线,
∴BD=CD,
∴S△ADB=S△ADC;
(2)由(1)可知S△ADB=S△ADC,
同理S△ABO=S△DBO=
| 1 |
| 2 |
∴S△ABO=
| 1 |
| 4 |
即S1=
| 1 |
| 4 |
栽种花卉(阴影部分)的面积是
| 1 |
| 4 |
故答案为:10.
点评:考查了三角形的面积和三角形中线的性质,三角形中线将三角形分成面积相等的两部分.

练习册系列答案
相关题目
 28、如图,点D为线段BC中点,AB=AC,求证:∠B=∠C.(利用全等方法证明)
28、如图,点D为线段BC中点,AB=AC,求证:∠B=∠C.(利用全等方法证明)

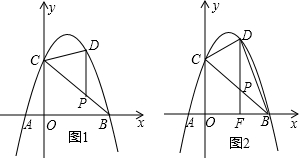 (2013•许昌一模)抛物线y=ax2+bx+3经过点A、B、C,已知A(-1,0),B(3,0).
(2013•许昌一模)抛物线y=ax2+bx+3经过点A、B、C,已知A(-1,0),B(3,0).