题目内容
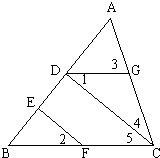 20、已知:如图,CD⊥AB,垂足为D,点F是BC上任意一点,FE⊥AB,垂足为E,且∠1=∠2=30°,∠3=84°,求∠4的度数.
20、已知:如图,CD⊥AB,垂足为D,点F是BC上任意一点,FE⊥AB,垂足为E,且∠1=∠2=30°,∠3=84°,求∠4的度数.解:∵CD⊥AB,FE⊥AB(已知)
∴∠CDB=∠FEB=90°(垂直的定义)
∴
CD
∥EF
∴∠5=∠
2
∵∠1=∠2(已知)
∴∠5=∠
1
=30°(等量代换)
∴
DG
∥BC
∴∠BCA=∠3=
84
°(两直线平行,同位角相等)
∴∠4=∠BCA-∠5=
54
°.分析:根据同时垂直于同一条直线的两条直线平行推知CD∥EF,所以同位角∠5=∠2;然后由已知条件∠1=∠2、等量代换求得内错角∠5=∠1=30°,所以两直线DG∥BC,∴同位角∠BCA=∠3=84°;最后由等量代换求得∠4=∠BCA-∠5=54°.
解答:解:∵CD⊥AB,FE⊥AB(已知)
∴∠CDB=∠FEB=90°(垂直的定义)
∴CD∥EF
∴∠5=∠2(两直线平行,同位角相等)
∵∠1=∠2(已知)
∴∠5=∠1=30°(等量代换),
∴DG∥BC (内错角相等,两直线平行)
∴∠BCA=∠3=84° (两直线平行,同位角相等),
∴∠4=∠BCA-∠5=54°.
故答案是:CD、EF、2、1、等量代换、DG、BC、84、54.
∴∠CDB=∠FEB=90°(垂直的定义)
∴CD∥EF
∴∠5=∠2(两直线平行,同位角相等)
∵∠1=∠2(已知)
∴∠5=∠1=30°(等量代换),
∴DG∥BC (内错角相等,两直线平行)
∴∠BCA=∠3=84° (两直线平行,同位角相等),
∴∠4=∠BCA-∠5=54°.
故答案是:CD、EF、2、1、等量代换、DG、BC、84、54.
点评:本题考查了平行线的判定与性质.解答此题的关键是注意平行线的性质和判定定理的综合运用.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
 4、已知:如图,CD⊥AB,BE⊥AC,垂足分别为D、E,BE、CD相交于O点,∠1=∠2.图中全等的三角形共有( )
4、已知:如图,CD⊥AB,BE⊥AC,垂足分别为D、E,BE、CD相交于O点,∠1=∠2.图中全等的三角形共有( ) 22、已知,如图,CD平分∠ACB,AC∥DE,CD∥EF,求证:EF平分∠DEB.
22、已知,如图,CD平分∠ACB,AC∥DE,CD∥EF,求证:EF平分∠DEB.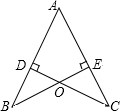 已知:如图,CD⊥AB于点D,BE⊥AC于点E,BE与CD交于点O,且BD=CE.
已知:如图,CD⊥AB于点D,BE⊥AC于点E,BE与CD交于点O,且BD=CE. 已知:如图,CD⊥AB于点D,BE⊥AC于点E,BE、CD交于点O,且AO平分∠BAC.那么OB与OC相等吗?谈谈你的理由.
已知:如图,CD⊥AB于点D,BE⊥AC于点E,BE、CD交于点O,且AO平分∠BAC.那么OB与OC相等吗?谈谈你的理由. 已知:如图AB∥CD,CE平分∠ACD,∠A=110°,则∠ECD等于
已知:如图AB∥CD,CE平分∠ACD,∠A=110°,则∠ECD等于