题目内容
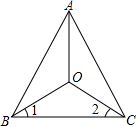 如图,已知OA平分∠BAC,∠1=∠2,求证:△AOB≌△AOC.
如图,已知OA平分∠BAC,∠1=∠2,求证:△AOB≌△AOC.分析:如图,作OE⊥AB于E,OF⊥AC于F,通过Rt△OBE≌Rt△OCF(HL)来证AB=AC.最后根据全等三角形的判定定理SAS证得结论.
解答: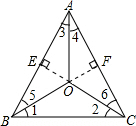 证明:如图,作OE⊥AB于E,OF⊥AC于F,
证明:如图,作OE⊥AB于E,OF⊥AC于F,
∵AO平分∠BAC,
∴OE=OF(角平分线上的点到角两边的距离相等).
∵∠1=∠2,
∴OB=OC.
∴在Rt△OBE与Rt△OCF中,
,
∴Rt△OBE≌Rt△OCF(HL).
∴∠5=∠6.
∴∠1+∠5=∠2+∠6.
即∠ABC=∠ACB.
∴AB=AC.
∴在△AOB与△AOC中,
,
∴:△AOB≌△AOC(SAS).
 证明:如图,作OE⊥AB于E,OF⊥AC于F,
证明:如图,作OE⊥AB于E,OF⊥AC于F,∵AO平分∠BAC,
∴OE=OF(角平分线上的点到角两边的距离相等).
∵∠1=∠2,
∴OB=OC.
∴在Rt△OBE与Rt△OCF中,
|
∴Rt△OBE≌Rt△OCF(HL).
∴∠5=∠6.
∴∠1+∠5=∠2+∠6.
即∠ABC=∠ACB.
∴AB=AC.
∴在△AOB与△AOC中,
|
∴:△AOB≌△AOC(SAS).
点评:本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
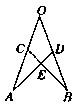 8、如图,已知OA=OB,OC=OD,下列结论中:①∠A=∠B;②DE=CE;③连OE,则OE平分∠O,正确的是( )
8、如图,已知OA=OB,OC=OD,下列结论中:①∠A=∠B;②DE=CE;③连OE,则OE平分∠O,正确的是( ) 如图,已知OA⊥OD,BO平分∠AOC,∠AOB:∠COD=2:5.求∠AOB的度数.
如图,已知OA⊥OD,BO平分∠AOC,∠AOB:∠COD=2:5.求∠AOB的度数.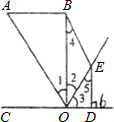 如图,已知OA∥BE,OB平分∠AOE,∠4=∠5,∠2与∠3互余;那么DE和CD有怎样的位置关系?为什么?
如图,已知OA∥BE,OB平分∠AOE,∠4=∠5,∠2与∠3互余;那么DE和CD有怎样的位置关系?为什么?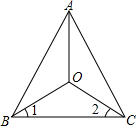 如图,已知OA平分∠BAC,∠1=∠2,求证:△AOB≌△AOC.
如图,已知OA平分∠BAC,∠1=∠2,求证:△AOB≌△AOC.