Question

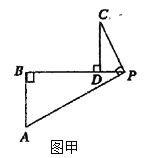
【题目】已知，如图，AB是的直径，C是上一点，连接AC，过点C作直线于D（），点E是DB上任意一点（点D、B除外），直线CE交于点F.连接AF与直线CD交于点G.

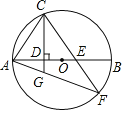
（1）求证：

（2）若点E是AD（点A除外）上任意一点，上述结论是否仍然成立？若成立，请画出图形并给予证明；若不成立，请说明理由。

Answer 1

【答案】（1）证明见解析；（2）成立，证明见解析.

【解析】

（1）欲证AC2=AGAF，即证AC：AG=AF：AC，可以通过证明△AGC∽△ACF得到；

（2）分清E点在AD上有两种情况，然后逐一证明．

（1）证明：连接CB，

∵AB是直径，CD⊥AB，

∴∠ACB=∠ADC=90°，又∠CAD=∠BAC，

∴△CAD∽△BAC，

∴∠ACD=∠ABC，

∵∠ABC=∠AFC，

∴∠ACD=∠AFC，∠CAG=∠FAC，

∴△ACG∽△AFC，

∴，

∴AC2=AGAF；

（2）当点E是AD（点A除外）上任意一点，上述结论仍成立

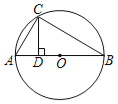
①当点E与点D重合时，F与G重合，如图所示：

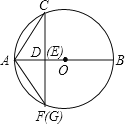
有AG=AF，∵CD⊥AB，

∴ ，AC=AF，

∴AC2=AGAF；

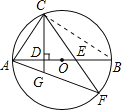
②当点E与点D不重合时（不含点A）时，如图所示：

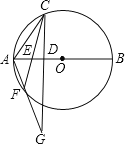
证明类似（1）．