题目内容
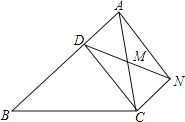
【题目】已知:如图,D是△ABC的边AB上一点,CN∥AB,DN交AC于点M,MA=MC.
①求证:CD=AN;
②若∠AMD=2∠MCD,求证:四边形ADCN是矩形.
【答案】(1)证明见解析;(2)证明见解析.
【解析】
试题分析:①根据两直线平行,内错角相等求出∠DAC=∠NCA,然后利用“角边角”证明△AMD和△CMN全等,根据全等三角形对应边相等可得AD=CN,然后判定四边形ADCN是平行四边形,再根据平行四边形的对边相等即可得证;
②根据三角形的一个外角等于与它不相邻的两个内角的和推出∠MCD=∠MDC,再根据等角对等边可得MD=MC,然后证明AC=DN,再根据对角线相等的平行四边形是矩形即可得证.
试题解析:①∵CN∥AB,
∴∠DAC=∠NCA,
在△AMD和△CMN中,
∠DAC=∠NCA
∵ MA=MC ,
∠AMD=∠CMN
∴△AMD≌△CMN(ASA),
∴AD=CN,
又∵AD∥CN,
∴四边形ADCN是平行四边形,
∴CD=AN;
②∵∠AMD=2∠MCD,∠AMD=∠MCD+∠MDC,
∴∠MCD=∠MDC,
∴MD=MC,
由①知四边形ADCN是平行四边形,
∴MD=MN=MA=MC,
∴AC=DN,
∴四边形ADCN是矩形.

【题目】为了保护环境,某开发区综合治理指挥部决定购买A,B两种型号的污水处理设备共10台.已知用90万元购买A型号的污水处理设备的台数与用75万元购买B型号的污水处理设备的台数相同,每台设备价格及月处理污水量如下表所示:
污水处理设备 | A型 | B型 |
价格(万元/台) | m | m-3 |
月处理污水量(吨/台) | 220 | 180 |
(1)求m的值;
(2)由于受资金限制,指挥部用于购买污水处理设备的资金不超过165万元,问有多少种购买方案?并求出每月最多处理污水量的吨数.