题目内容
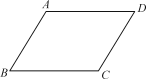
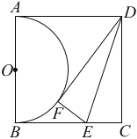
【题目】如图,正方形![]() 的边长为2,点
的边长为2,点![]() 是
是![]() 边上的一点,以
边上的一点,以![]() 为直径在正方形内作半圆
为直径在正方形内作半圆![]() ,将
,将![]() 沿着
沿着![]() 翻折,点
翻折,点![]() 恰好落在半圆
恰好落在半圆![]() 上的点
上的点![]() 处,则
处,则![]() 的长为( )
的长为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
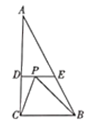
连接OD,OF,判定△AOD≌△FOD,可得∠DAO=∠DFO=90°,O,F,E在同一直线上,设CE=EF=x,则BE=2-x,OE=1+x,依据勾股定理可得Rt△BOE中,BO2+BE2=OE2,列方程即可得到CE的长.
解:如图,连接OD,OF,
由AO=FO=1,AD=FD,DO=DO,可得△AOD≌△FOD,
∴∠DAO=∠DFO=90°,
又∵∠DFE=∠C=90°,
∴O,F,E在同一直线上,
设CE=EF=x,则BE=2-x,OE=1+x,
在Rt△BOE中,BO2+BE2=OE2,
∴12+(2-x)2=(1+x)2,
解得x=![]() ,
,
∴CE=![]() ,
,
故选D.


练习册系列答案
相关题目