题目内容
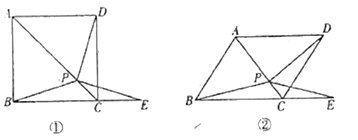
【题目】如图①,在正方形![]() 中,
中,![]() 是对角线
是对角线![]() 上的一点,点
上的一点,点![]() 在
在![]() 的延长线上,且
的延长线上,且![]()
![]() 求证:
求证:![]()
![]() 求证:
求证:![]()
![]() 把正方形
把正方形![]() 改为菱形,其他条件不变(如图
改为菱形,其他条件不变(如图![]() ②),且
②),且![]() ,求
,求![]() 的大小.
的大小.
【答案】(1)详见解析;(2)详见解析;(3)![]()
【解析】
(1)根据正方形的四条边都相等可得BC=DC,对角线平分一组对角可得∠BCP=∠DCP,然后利用“边角边”证明即可;
(2)根据全等三角形对应角相等可得∠CBP=∠CDP,根据等边对等角可得∠CBP=∠E,然后求出∠DPE=∠DCE,再根据两直线平行,同位角相等可得∠DCE=∠ABC,从而得证;
(3)仿照(1),(2)的证明过程,即可得到∠DPE=∠ABC=58°.
![]() 证明:
证明:![]() 正方形
正方形![]()
![]()
在![]() 和
和![]() 中
中
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 正方形
正方形![]()
![]()
![]()
![]() .
.
(3)在菱形ABCD中,BC=DC,∠BCP=∠DCP,
在△BCP和△DCP中,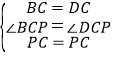 ,
,
∴△BCP≌△DCP(SAS),
∴∠CBP=∠CDP,
∵PE=PB,
∴∠CBP=∠E,
∴∠DPE=∠DCE,
∵AB∥CD,
∴∠DCE=∠ABC,
∴∠DPE=∠ABC=58°.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目