题目内容
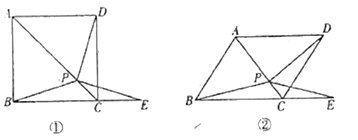
【题目】勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,其中的“面积法”给了小聪以灵感,他惊喜的发现,当两个全等的直角三角形如图1或图2摆放时,都可以用“面积法”来证明,下面是小聪利用图1证明勾股定理的过程:

将两个全等的直角三角形按图1所示摆放,其中∠DAB=90°,求证:a2+b2=c2
证明:连接DB,过点D作BC边上的高DF,则DF=EC=b﹣a.
∵S四边形ADCB=S△ACD+S△ABC=![]() b2+
b2+![]() ab.
ab.
又∵S四边形ADCB=S△ADB+S△DCB=![]() c2+
c2+![]() a(b﹣a)
a(b﹣a)
∴![]() b2+
b2+![]() ab=
ab=![]() c2+
c2+![]() a(b﹣a)
a(b﹣a)
∴a2+b2=c2
请参照上述证法,利用图2完成下面的证明.
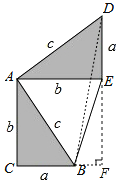
将两个全等的直角三角形按图2所示摆放,其中∠DAB=90°.求证:a2+b2=c2
证明:连结______,过点B作________,则____________.
∵S五边形ACBED=S△ACB+S△ABE+S△ADE=____________.
又∵S五边形ACBED=______________=![]() ab+
ab+![]() c2+
c2+![]() a(b﹣a),
a(b﹣a),
∴___________________=![]() ab+
ab+![]() c2+
c2+![]() a(b﹣a),
a(b﹣a),
∴a2+b2=c2.
【答案】BD;DE边上的高BF;BF=b-a;![]() ab+
ab+![]() b2+
b2+![]() ab;S△ACB+S△ABD+S△BDF;
ab;S△ACB+S△ABD+S△BDF;![]() ab+
ab+![]() b2+
b2+![]() ab.
ab.
【解析】
连结BD,过点B作DE边上的高BF,则BF=b-a,表示出S五边形ACBED,进而可得出答案.
证明:连结BD,过点B作DE边上的高BF,则BF=b-a,
∴S五边形ACBED=S△ACB+S△ABE+S△ADE=![]() ab+
ab+![]() b2+
b2+![]() ab,
ab,
又∵S五边形ACBED=S△ACB+S△ABD+S△BDE=![]() ab+
ab+![]() c2+
c2+![]() a(b-a),
a(b-a),
∴![]() ab+
ab+![]() b2+
b2+![]() ab=
ab=![]() ab+
ab+![]() c2+
c2+![]() a(b-a),
a(b-a),
∴a2+b2=c2.
故答案为:BD;DE边上的高BF;BF=b-a;![]() ab+
ab+![]() b2+
b2+![]() ab;S△ACB+S△ABD+S△BDF;
ab;S△ACB+S△ABD+S△BDF;![]() ab+
ab+![]() b2+
b2+![]() ab.
ab.

【题目】某公司从2014年开始投入技术改进资金,经技术改进后,其产品的成本不断降低,具体数据如下表:
年 度 | 2013 | 2014 | 2015 | 2016 |
投入技改资金 | 2.5 | 3 | 4 | 4.5 |
产品成本 | 7.2 | 6 | 4.5 | 4 |
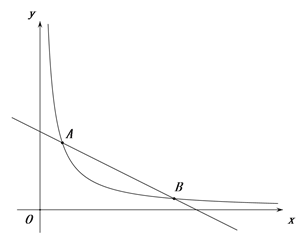
(1)请你认真分析表中数据,从一次函数和反比例函数中确定哪一个函数能表示其变化规律,给出理由,并求出其解析式;
(2)按照这种变化规律,若2017年已投入资金5万元.
①预计生产成本每件比2016年降低多少万元?
②若打算在2017年把每件产品成本降低到3.2万元,则还需要投入技改资金多少万元?(结果精确到0.01万元).