Question

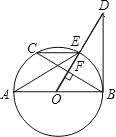
【题目】如图，已知△ABC，

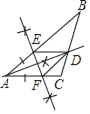
（1）尺规作图：作AD平分∠BAC交BC于D点，再作AD的垂直平分线交AB于E点，交AC于F点（保留作图痕迹，不写作法）；

（2）连接DE，DF证明：四边形AEDF是菱形；

（3）若BE＝7，AF＝4，CD＝3，求BD的长．

Answer 1

【答案】（1）作图见解析；（2）证明见解析；（3）BD＝；

【解析】

（1）∠BAC的平分线AD，线段AD的垂直平分线MN，分别交AB、AC于点E、F，如图所示；

（2）EF是线段AD的垂直平分线得出AE＝DE，AF＝DF，再由AD平分∠BAC证得∠EDA＝∠CAD，所以DE∥AC即可证明平行四边形AEDF是菱形；

（3）由（2）AEDF是菱形，推出AE=DE=AF=DF=4，由DE∥AC，推出由此即可解决问题．

（1）作图如下：

（2）∵根据作法可知：EF是线段AD的垂直平分线，

∴AE＝DE，AF＝DF，

∴∠EAD＝∠EDA，

∵AD平分∠BAC，

∴∠BAD＝∠CAD，

∴∠EDA＝∠CAD，

∴DE∥AC，

同理可得：DF∥AE，

∴四边形AEDF是平行四边形，

∵AE＝DE，

∴平行四边形AEDF是菱形；

（3）∵AEDF是菱形，

∴AE＝DE＝DF＝AF，

∵AF＝4，

∴AE＝DE＝DF＝AF＝4，

∵DE∥AC，

∴

∴＝，

解得：BD＝．