题目内容
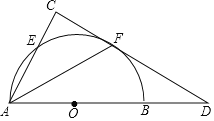
【题目】如图(1),已知正方形ABCD在直线MN的上方BC在直线MN上,E是BC上一点,以AE为边在直线MN的上方作正方形AEFG.
(1)连接GD,求证:△ADG≌△ABE;
(2)连接FC,观察并直接写出∠FCN的度数(不要写出解答过程)
(3)如图(2),将图中正方形ABCD改为矩形ABCD,AB=6,BC=8,E是线段BC上一动点(不含端点B、C),以AE为边在直线MN的上方作矩形AEFG,使顶点G恰好落在射线CD上.判断当点E由B向C运动时,∠FCN的大小是否总保持不变,若∠FCN的大小不变,请求出tan∠FCN的值.若∠FCN的大小发生改变,请举例说明.
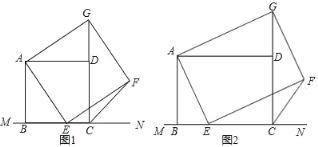
【答案】(1)见解析;(2)∠FCN=45°,理由见解析;(3)当点E由B向C运动时,∠FCN的大小总保持不变,tan∠FCN=![]() .理由见解析.
.理由见解析.
【解析】
(1)根据三角形判定方法进行证明即可.
(2)作FH⊥MN于H.先证△ABE≌△EHF,得到对应边相等,从而推出△CHF是等腰直角三角形,∠FCH的度数就可以求得了.
(3)解法同(2),结合(1)(2)得:△EFH≌△GAD,△EFH∽△ABE,得出EH=AD=BC=8,由三角函数定义即可得出结论.
(1)证明:∵四边形ABCD和四边形AEFG是正方形,
∴AB=AD,AE=AG=EF,∠BAD=∠EAG=∠ADC=90°,
∴∠BAE+∠EAD=∠DAG+∠EAD,∠ADG=90°=∠ABE,
∴∠BAE=∠DAG,
在△ADG和△ABE中,
 ,
,
∴△ADG≌△ABE(AAS).
(2)解:∠FCN=45°,理由如下:
作FH⊥MN于H,如图1所示:
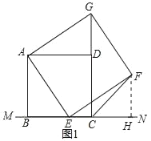
则∠EHF=90°=∠ABE,
∵∠AEF=∠ABE=90°,
∴∠BAE+∠AEB=90°,∠FEH+∠AEB=90°,
∴∠FEH=∠BAE,在△EFH和△ABE中,
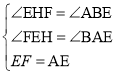 ,
,
∴△EFH≌△ABE(AAS),
∴FH=BE,EH=AB=BC,
∴CH=BE=FH,
∵∠FHC=90°,
∴∠FCN=45°.
(3)当点E由B向C运动时,∠FCN的大小总保持不变,理由如下:
作FH⊥MN于H,如图2所示:
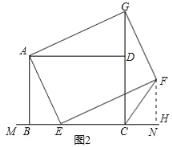
由已知可得∠EAG=∠BAD=∠AEF=90°,
结合(1)(2)得:△EFH≌△GAD,△EFH∽△ABE,
∴EH=AD=BC=8,
∴CH=BE,
∴![]() ;
;
在Rt△FEH中,tan∠FCN=![]() ,
,
∴当点E由B向C运动时,∠FCN的大小总保持不变,tan∠FCN=![]() .
.

 同步练习强化拓展系列答案
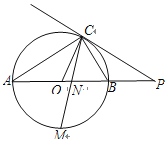
同步练习强化拓展系列答案【题目】如图,在△ABC中,E是AC边上的一点,且AE=AB,∠BAC=2∠CBE,以AB为直径作⊙O交AC于点D,交BE于点F.
(1)求证:BC是⊙O的切线;
(2)若AB=8,BC=6,求DE的长.
【题目】“五一”长假期间,某玩具超市设立了一个如图所示的可以自由转动的转盘,开展有奖购买活动,顾客购买玩具就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应奖品.下表是该活动的一组统计数据:
转动转盘的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
落在“铅笔”区域的次数m | 68 | 108 | 140 | 355 | 560 | 690 |
落在“铅笔”区域的频率 | 0.68 | 0.72 | 0.70 | 0.71 | 0.70 | 0.69 |
下列说法不正确的是( )

A. 当n很大时,估计指针落子在”铅笔“区域的概率大约是0.70
B. 假如你去转动转盘一次,获得“铅笔”概率大约是0.70
C. 如果转动转盘3000次,指针落在“文具盒”区域的次数大约有900次
D. 转动转盘20次,一定有6次获得“文具盒”