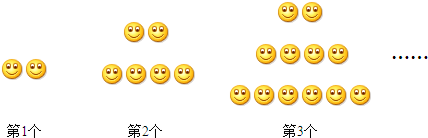题目内容
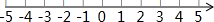 (2013•宁德)(1)计算:
(2013•宁德)(1)计算:| a |
| a-b |
| a2-b2 |
| a |
(2)解不等式组,并把它的解集表示在数轴上;
|
分析:(1)先算乘法,再算减法,即可得出答案.
(2)求出两个不等式的解集,根据找不等式组解集的规律找出即可.
(2)求出两个不等式的解集,根据找不等式组解集的规律找出即可.
解答:解:(1)原式=
•
-b
=
•
-b
=a+b-b
=a.
(2)∵解不等式3x>2x-1得:x>-1,
解不等式2(x-1)≤6得:x≤4,
∴不等式组的解集是-1<x≤4,
在数轴上表示不等式组的解集为: .
.
| a |
| a-b |
| a2-b2 |
| a |
=
| a |
| a-b |
| (a+b)(a-b) |
| a |
=a+b-b
=a.
(2)∵解不等式3x>2x-1得:x>-1,
解不等式2(x-1)≤6得:x≤4,
∴不等式组的解集是-1<x≤4,
在数轴上表示不等式组的解集为:
 .
.点评:本题考查了分式的混合运算和解一元一次不等式组的应用,主要考查学生的化简和计算能力.

练习册系列答案
相关题目
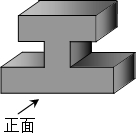 (2013•宁德质检)如图所示几何体的俯视图是( )
(2013•宁德质检)如图所示几何体的俯视图是( )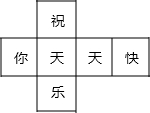 (2013•宁德质检)一个材质均匀的正方体六个面上分别标有文字”祝、你、天、天、快、乐”掷这个正方体,结果的其表面展开图如图所示,随机抛“天”字朝上的概率是( )
(2013•宁德质检)一个材质均匀的正方体六个面上分别标有文字”祝、你、天、天、快、乐”掷这个正方体,结果的其表面展开图如图所示,随机抛“天”字朝上的概率是( ) 按一定的规律组成,其中第1个图形有2个,第 2个图形中有6个,第3个图形中有12个…,则第30个图形中
按一定的规律组成,其中第1个图形有2个,第 2个图形中有6个,第3个图形中有12个…,则第30个图形中 的个数是( )
的个数是( )