题目内容
在一幅长60cm,宽40cm的矩形风景画的四周镶一条宽度相等的金色纸边,制成一幅矩形挂图,如图所示,如果要使整个挂图的面积是2816cm2,设金色纸边的宽为xcm,那么x满足的方程是


| A.(60+x)(40+2x)=2816 | B.(60+x)(40+x)=2816 |
| C.(60+2x)(40+x)=2816 | D.(60+2x)(40+2x)=2816 |
D
根据题意可知:矩形挂图的长为(60+2x)cm,宽为(40+2x)cm;则运用面积公式列方程即可.
解:挂图长为(60+2x)cm,宽为(40+2x)cm,
所以根据矩形的面积公式可得:(60+2x)(40+2x)=2816.
故选D.
此题是一元二次方程的应用,解此类题的关键是看准题型列面积方程,矩形的面积=矩形的长×矩形的宽.
解:挂图长为(60+2x)cm,宽为(40+2x)cm,
所以根据矩形的面积公式可得:(60+2x)(40+2x)=2816.
故选D.
此题是一元二次方程的应用,解此类题的关键是看准题型列面积方程,矩形的面积=矩形的长×矩形的宽.

练习册系列答案
相关题目
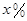 后售价价为127元,下面所列方程中正确的是( )
后售价价为127元,下面所列方程中正确的是( )




 .若商店在试销期间每天销售这种商品获得200元的利润,根据题意,下面所列方程正确的是( ).
.若商店在试销期间每天销售这种商品获得200元的利润,根据题意,下面所列方程正确的是( ).



 +n2+2m-6n+10=0的是( )
+n2+2m-6n+10=0的是( )